时间：   |   分类：     |   阅读： 790 字 ~4分钟

本文为Social Network Analysis学习笔记，课程地址为https://www.coursera.org/course/sna。

第一讲：SNA工具

Gephi

Gephi - The Open Graph Viz Platform

社交网络分析：SNA工具

iGraph

社交网络分析：SNA工具

Pajek

社交网络分析：SNA工具 

UCINet

社交网络分析：SNA工具

NodeXL

社交网络分析：SNA工具

  • http://nodexl.codeplex.com/
  • 交互式网络可视化和分析工具，以MS Excel模板的形式利用MSExcel作为数据展示和分析平台。可以定制图像外观、无损缩放、移动图像，动态过滤顶点和边，提供多种布局方式，查找群和相关边，支持多种数据格式输入和输出。
  • 开源，支持Windows Excel 2007/2010/2013
  • NodeXL文档

其他

R

Python

Java

  • Jung（Java Universal Network/Graph Framework）：Java平台网络/图应用开发的一种通用基础架构。其目的在于为开发关于图或网络结构的应用程序提供一个易用、通用的基础架构。使用JUNG功能调用，可以方便的构造图或网络的数据结构，应用经典算法（如聚类、最短路径，最大流量等），编写和测试用户自己的算法，以及可视化的显示数据的网络图。
  • Neo4j：图数据库
  • Blueprints：类似于JDBC，但是用于图数据库
  • SoNIA（Social Network Image Animator）:用于动态或纵向数据的可视化。

JavaScript

  • D3.js： 数据驱动的文档（Data DrivenDocuments）
  • JSNetworkX：NetworkX图形库在JavaScript上的移植版本。
  • arbor.js：使用webworkers和jQuery的图形可视化库。

社交网挖掘

Talend

Twitter

LinkedIn

第二讲：网络介绍

网络定义

网络就是由边(edge)所连接的一些点(node)。
"网络"≡"图"
点线
verticesedges, arcs数学
nodeslinks计算机科学
sitesbonds物理学
actorsties, relations社会学
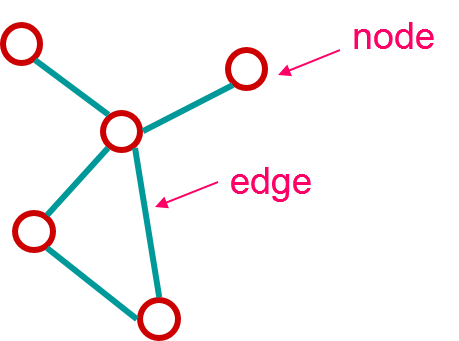![社交网络分析：网络介绍](/images/2014/10/0026uWfMgy6O7qbbpnuec.png)

边

方向：

  • 单向的 A->B (例如A likesB; A gave agift to B; Ais B’s child)
  • 双向的 A<->B 或 A-B (例如A and Blike each other; A and B aresiblings; Aand B are co-authors)

属性：

  • 权重(例如通信频率)
  • 排名(第一好友、第二好友…)
  • 类型(朋友、亲戚、同事)
  • 取决于剩余图结构的属性：例如betweenness

图的数据表达方式

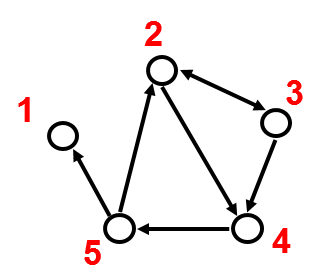
社交网络分析：网络介绍

|相邻矩阵(adjacency matrix)|边列表
(edge list)|相邻列表(adjacency list) |— |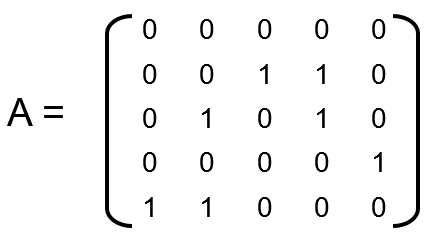社交网络分析：网络介绍|2, 3
2, 4
3, 2
3, 4
4, 5
5, 2
5, 1|如果网络很大或疏松的话，相邻列表易于实现。
可以为某个节点快速获取所有邻居节点。
1:
2: 3 4
3: 2 4
4: 5
5: 1 2

网络指标：节点度 (degree)

节点度是指和该节点相关联的边的个数。特别地，对于有向图，节点的入度是指进入该节点的边的个数；节点的出度是指从该节点出发的边的个数。

网络指标：节点度序列

每个节点的(入、出)度有序列表。

|度列表|图 |— |入度序列:[2, 2, 2, 1, 1, 1, 1, 0]
出度序列:[2, 2, 2, 2, 1, 1, 1, 0]
度序列:[3, 3, 3, 2, 2, 1, 1, 1]|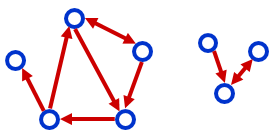社交网络分析：网络介绍

网络指标：节点度分布

每个节点度分布频度。

|度分布|图 |— |入度分布:[(2,3) (1,4) (0,1)]
出度分布:[(2,4) (1,3) (0,1)]
度分布:[(3,3) (2,2) (1,3)]|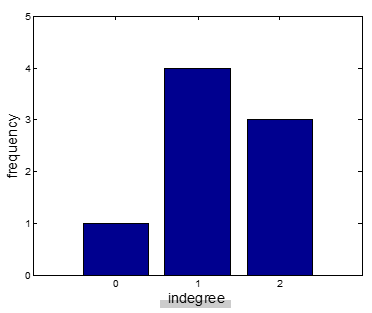社交网络分析：网络介绍

网络指标-连通分量(connectedcomponent)

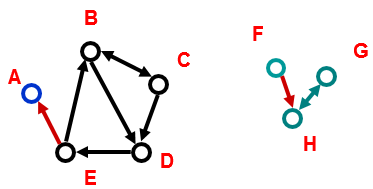社交网络分析：网络介绍 强连通分量：分量中每个节点都可以通过有向链接彼此可达。 示例中存在的强连通分量：

  • B C D E
  • A
  • G H
  • F

弱连通分量：分量中每个节点都可以通过任意方向链接彼此可达。 示例中存在的弱连通分量：

  • A B C D E
  • G H F

无向图中一般简单称之为连通分量。

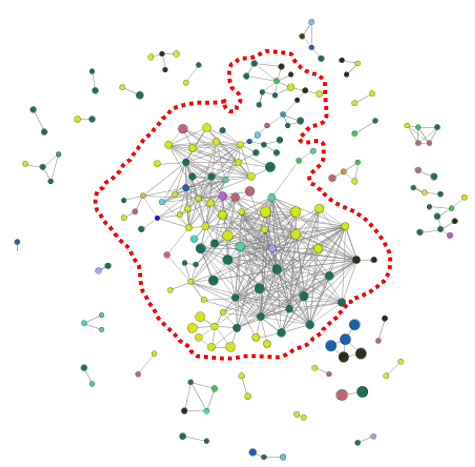
巨分量(Giant component)

如果最大的分量占整个图的显著部分，可被称为巨分量。 社交网络分析：网络介绍

第三讲：随机网络模型

网络模型

为什么建立网络模型？

  • 复杂网络的简单表达
  • 可以通过数学推导出属性
  • 可以预测属性和输出
  • 可以对比真实网络与假设模型的不同之处，从中获得顿悟

随机图模型：Erdös-Renyi模型

社交网络分析：随机网络模型

假设

  • 节点随机连接
  • 网络是无向网络

除了节点数N之外的关键参数：p或M

  • p=任意两个节点连接的概率
  • M=图中边的总数

度分布

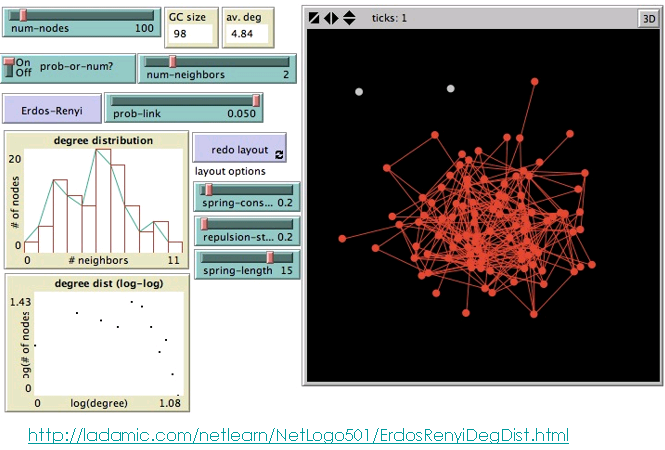
(N,p)模型：对每个潜在的边，概率p添加边，概率(1-p)不添加边。 社交网络分析：随机网络模型

每节点边数

每个节点最多可能（N-1）条边，每条边以概率p的可能性存在。二项分布提供了节点具有度K的概率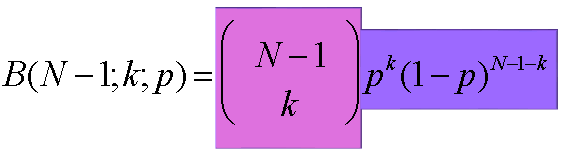： 社交网络分析：随机网络模型度的平均数为：z = (n-1)*p度的方差为：s2=(n-1)p(1-p)近似值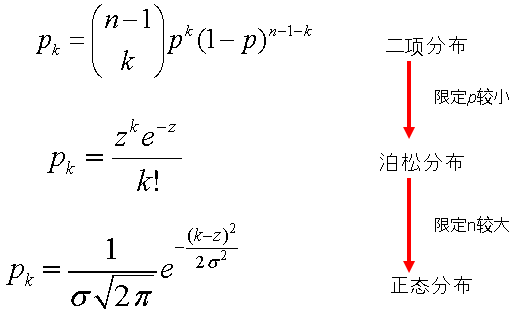：社交网络分析：随机网络模型

ER图模型认知

社交中心(hub)

该模型下无法获得大的社交中心。

巨分量

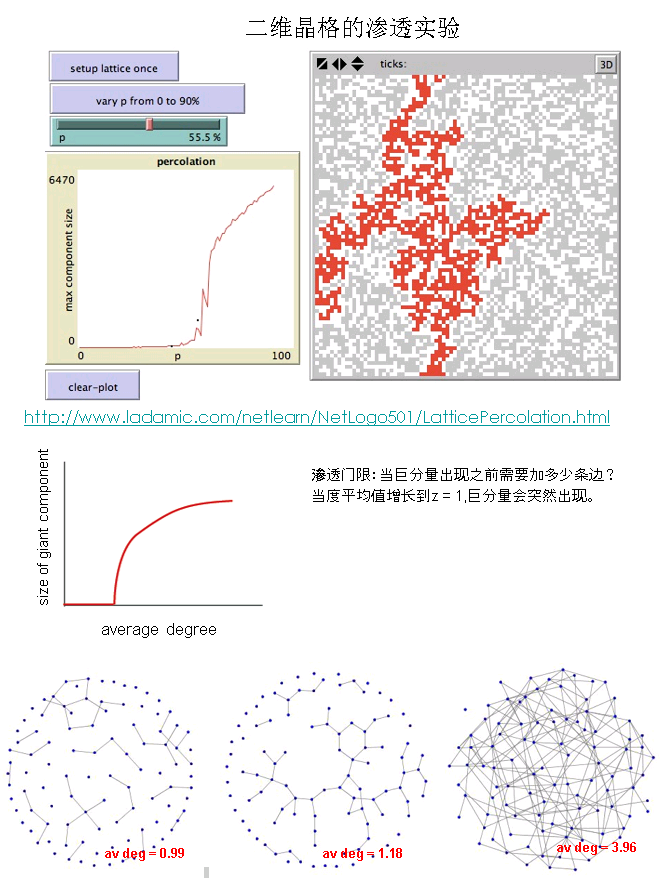社交网络分析：随机网络模型 上述实验中，每个点有可变的概率P表示渗透。当P等于1/2的时候，图中会出现一个明显的巨分量。

平均最短路径

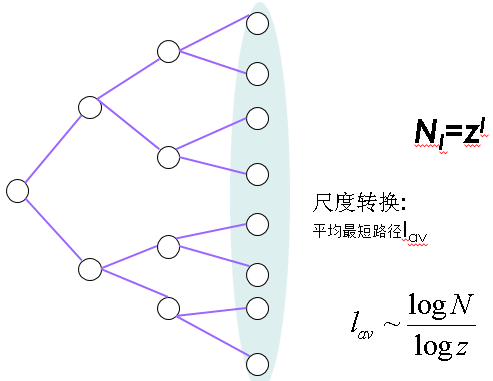
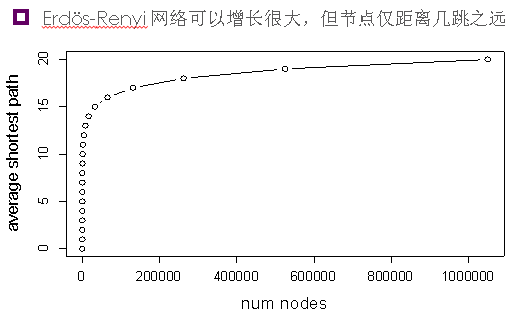
每对节点的平均跳数是多少？假如你的朋友与z（=度平均值）个你的其他朋友相连，忽略回路的话与你距离l跳的人有zl个。 社交网络分析：随机网络模型社交网络分析：随机网络模型

介绍模型(Introduction Model)

任意两个节点连接的概率prob-link仍然是p，此外增加了连接邻居节点的邻居节点概率prob-intro，不再完全随机。 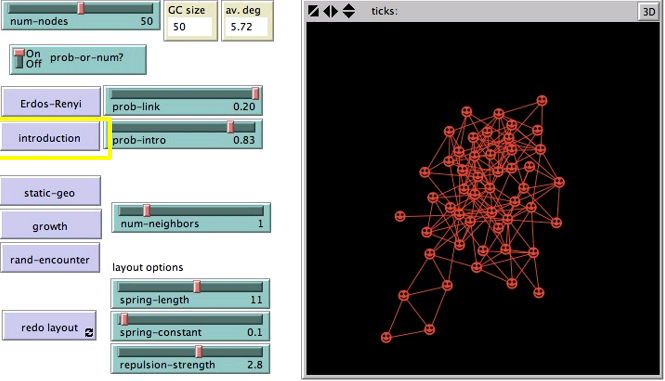社交网络分析：随机网络模型 与ER模型相比，介绍模型具有：

  • 更多的闭三点组（朋友将他的朋友介绍给你）
  • 更长的平均最短距离（边更局部连接）
  • 更多不均匀的度分布（有更多连接的节点更容易增加边）
  • 低概率p的情况更小的巨分量

静态地理模型(Static Geographical model)

每个节点与最接近的节点中的num-neighbors个相连。 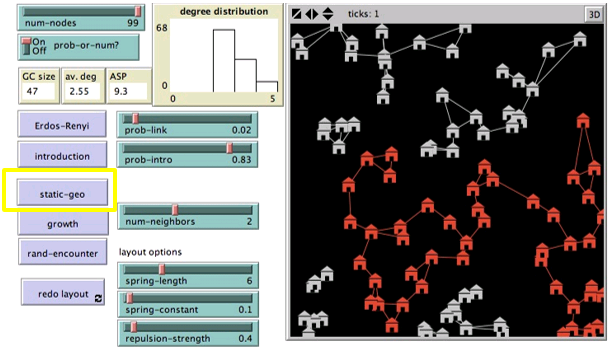社交网络分析：随机网络模型 与ER模型相比，静态地理模型具有：

  • 更窄的度分布(每个节点邻居节点目标一样，num-neighbors)
  • 更长的平均最短距离（地理局部连接）
  • 更小的巨分量(更少的机会进行随机连接)

随机遭遇模型(Random encounter)

节点随机移动，与偶遇的节点相连。 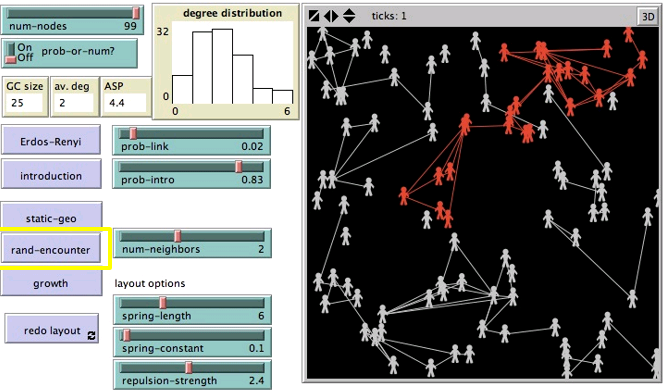社交网络分析：随机网络模型 与ER模型相比，随机遭遇模型具有：

  • 更长的平均最短距离
  • 更小的巨分量
  • 更多的闭三点组

生长模型(Growth model)

不是一开始就是固定数目节点，节点数随着时间增加。 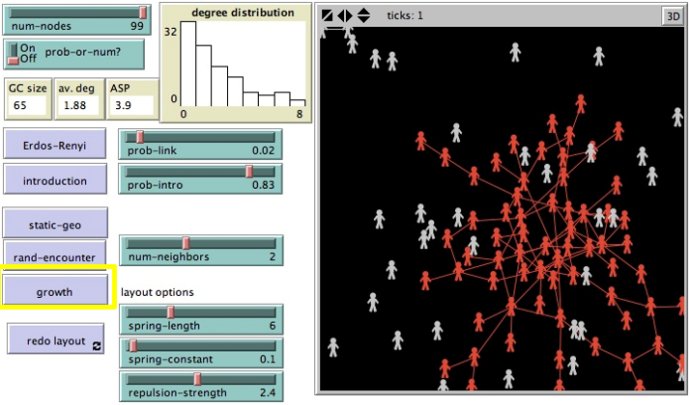社交网络分析：随机网络模型 与ER模型相比，生长模型具有：

  • 很多节点度为1
  • 没有很多闭三点组
  • 更小的巨分量
  • 老节点比新节点有更多的边

真实网络度分布

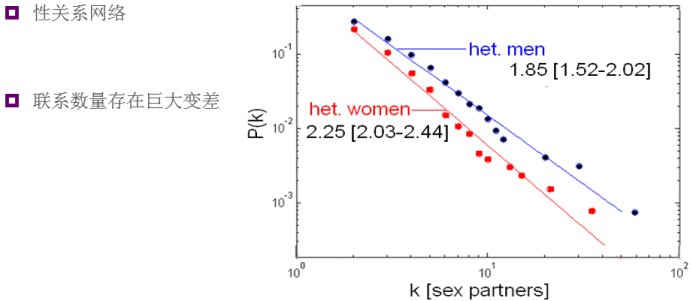
社交网络分析：随机网络模型

幂律分布分布

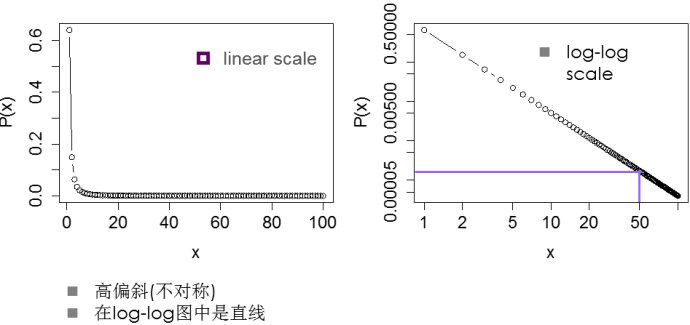社交网络分析：随机网络模型 度值为k的概率：p(k)= C * k ^ (-α)。C是标准化常数以使所有k的概率和为1。log(p(k)) = c - α *log(k)。

泊松分布

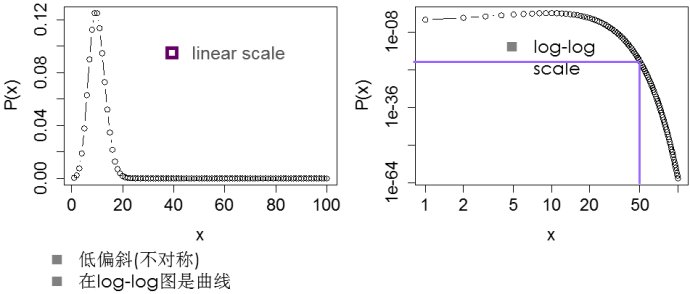
社交网络分析：随机网络模型

偏好性连接模型（preferential attachment）

节点更倾向与有更多边的节点连接，也被称为积累优势、富者愈富、马太效应。偏好性连接加剧了度分布的偏斜，使其具有幂律特性，指数α =2+1/m

Barabasi-Albert模型

开始用于描述万维网倾斜度分布。每个节点同其他节点以和对方度正比的概率相连。

  • 该过程起始有某个初始子图
  • 每个新节点将会有m个边
  • 连接节点i的概率结果是幂律分布其指数α =3

BA模型属性

  • 分布是尺度无关的，其指数α =3P(k) = 2 m2/k3
  • 图是连通的。一开始的图是连通的，
  • 新节点一出现就会有一到数个边（取决于m），它会同老节点相连，同时也会通过介绍与其他节点相连
  • 老节点更富有节点随着时间积累连接，从而使老节点更有优势，因为新节点偏好性连接而老节点会有更高的度值。

BA模型中新老节点的对比

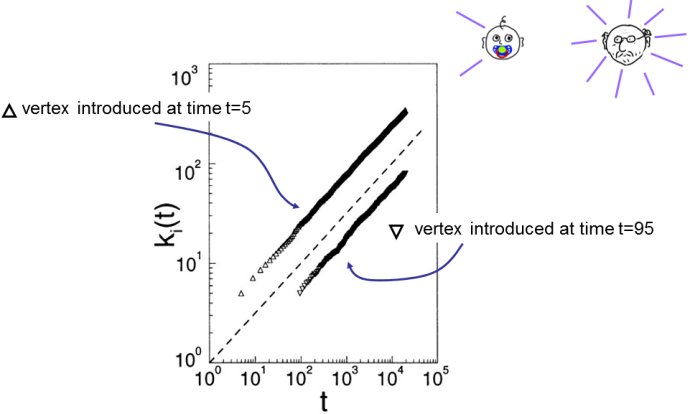
社交网络分析：随机网络模型

第四讲：网络中心性

对于中心性(centrality)的不同观点

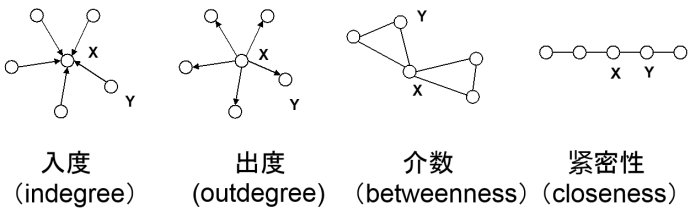
在下面每一个网络中，X都相对Y具有更高的中心性。 社交网络分析：网络中心性

定量度中心性

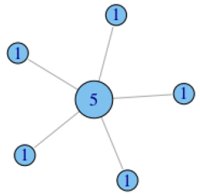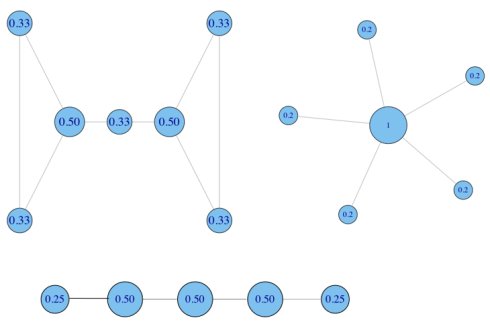
在每个节点上标注节点度。例如，拥有朋友越多的节点其中心性越高。 社交网络分析：网络中心性 其标准化就是用节点度除以最大的连接可能(N-1)。 社交网络分析：网络中心性

集中度(centralization)

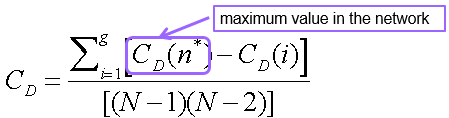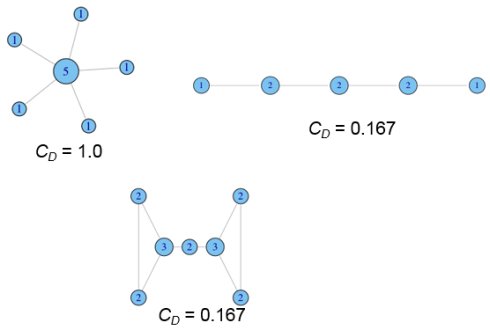
节点间的集中度分数存在多少差异？Freeman的集中度通用公式(可使用其他指标，如基尼系数或标准差) 社交网络分析：网络中心性 度集中度示例： 社交网络分析：网络中心性

介数(betweenness)

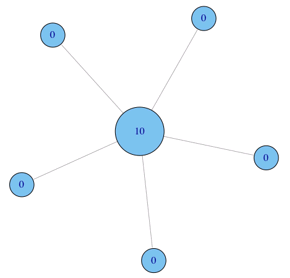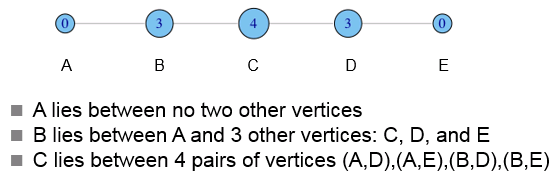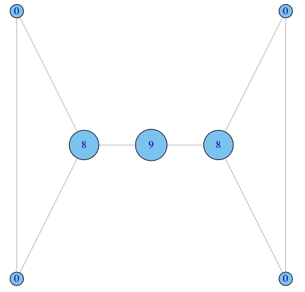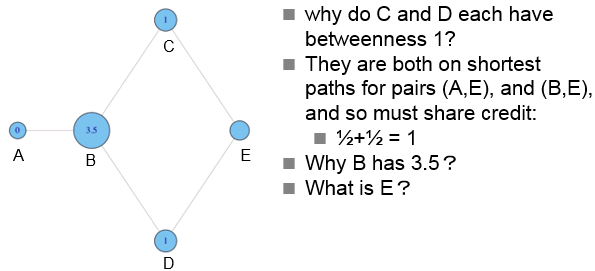
直观：多少个节点对必须经由本节点实现最小跳数互达。 定义： 社交网络分析：网络中心性 非标准化版本示例1： 社交网络分析：网络中心性 非标准化版本示例2： 社交网络分析：网络中心性 非标准化版本示例3： 社交网络分析：网络中心性 非标准化版本示例4： 社交网络分析：网络中心性 社交网络分析：网络中心性 经由B的最短路径有(A,C)、(A,E)、(A,D)，此外(C,D)的最短路径分配给B和E各0.5，因此B为3.5，E为0.5。

紧密性(closeness)

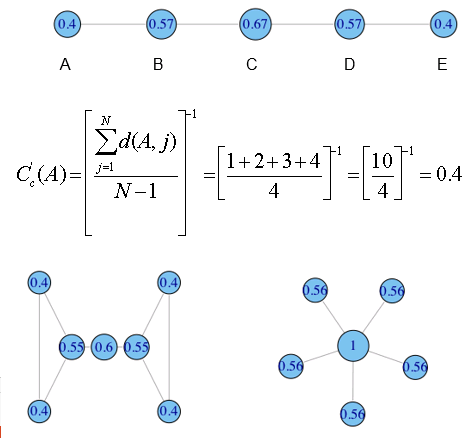
紧密性基于节点与网络所有其他节点的平均最短路径长度计算而得。 社交网络分析：网络中心性 示例： 社交网络分析：网络中心性

特征向量中心性(eigenvector centrality)

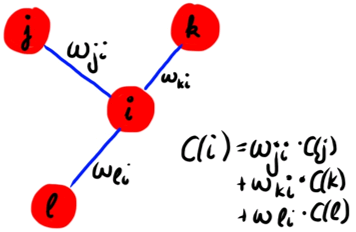
当前节点的中心性取决于邻居节点们的中心性。 社交网络分析：网络中心性

Bonacich特征向量中心性

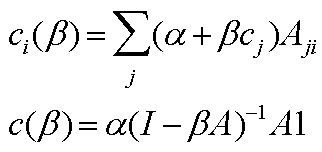
社交网络分析：网络中心性

  • a是一标准化常数
  • b决定邻居节点对中心性的重要性
  • A是相邻矩阵(可被权重)
  • I是单位矩阵
  • 1是全一的矩阵

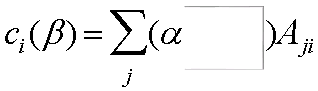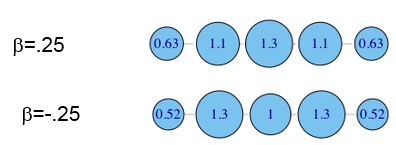
衰减因子b： 小b -> 高衰减：仅直接朋友起作用，且其重要性仅被考虑进去一点点。 高b -> 低衰减：全局网络(朋友，朋友的朋友等等)起作用 =0 产生简单的度中心性 社交网络分析：网络中心性 如果b>0,节点连接其他中心节点具有更高中心性。 如果b<0, 节点连接其他非中心节点具有更高中心性。 示例： 社交网络分析：网络中心性

有向网络的介数中心性

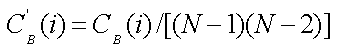
社交网络分析：网络中心性 唯一的修改：当标准化时将使用(N-1)(N-2)而不是(N-1)(N-2)/2。 社交网络分析：网络中心性

有向网络的紧密性中心性

选择一个方向：入紧密性、出紧密性。

有向网络的特征向量中心性

讲了pagerank和teleport。

中心性应用

以Java论坛为例，介绍了各种分析。

幂定律分布

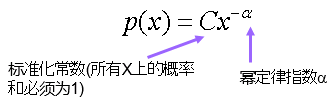
在log-log图中是一条直线：ln(p(x))=c-aln(x) 社交网络分析：网络中心性

参考

中心性(centrality)
Bonacich’s Centrality

第五讲：社区结构

为什么关注群体凝聚力？

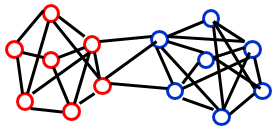
观点的形成和一致性：如果节点采用邻居节点的主流观点，就有可能不同有凝聚力的子组有不同的观点。 社交网络分析：社区结构

什么导致社区的形成？

  • 联系的相互关系(mutuality of ties)：组内每个人都认识其他人。
  • 成员间联系的频率：组内每个人都同组内的其他人存在至少k个连接。
  • 子组成员的亲密性或可达性：个体间被最多n跳分割。
  • 子组成员间相对非成员的相对联系频率。

归属网络(Affiliation networks)

小集团/帮派(cliques)

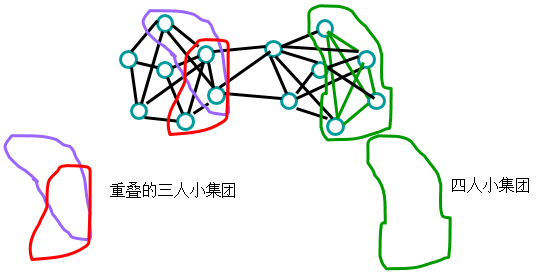
组内的每个成员都同其他成员有连接。小集团可以重叠。 社交网络分析：社区结构

小集团的意义

  • 不健壮：缺失一个连接将毁掉小集团
  • 无趣：每个人都同其他人连接；没有核心-边缘结构；无法使用中心性指标
  • 小集团如何重叠比自身更有趣

k-cores

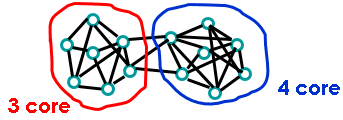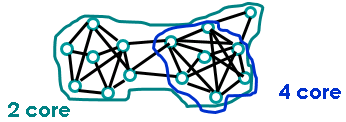
每个节点同组内k个其他节点相连。与小集团相比，简单且不那么严格。 社交网络分析：社区结构 即使如此，对于识别自然社区还是过于严苛的要求。 社交网络分析：社区结构

n – cliques

基于可达性和直径进行子组划分。子组内每两个节点最大距离为n。 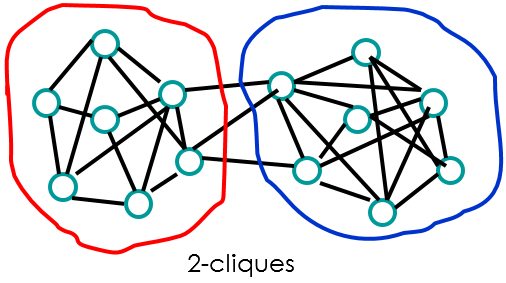社交网络分析：社区结构 问题：

  • 直径可能大于n
  • n-clique可能是断开的(路径通过子组外的节点进行)

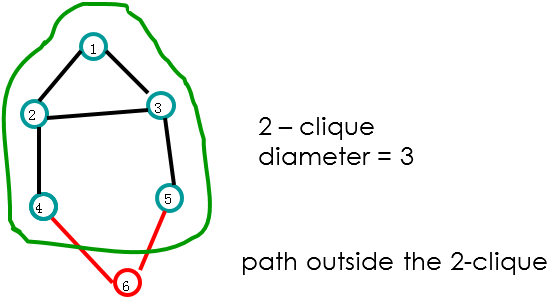社交网络分析：社区结构 解决方法：n-club:直径2的最大子图    {1,2,3,4},{1,2,3,5} and {2,3,4,5,6}

p-cliques

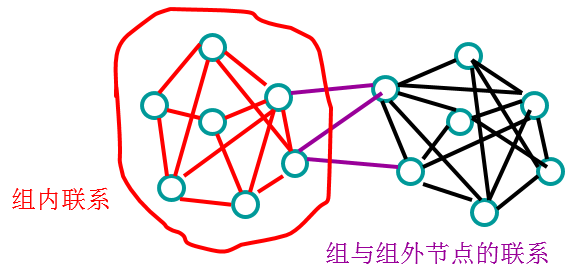
将网络分割成子组，其中节点至少有概率p的邻居节点在子组内。 社交网络分析：社区结构

有向加权网络的凝聚力

查找强连通分量 在查找强连通分量仅保留部分联系：相互的联系；边权重大于一定阀值。

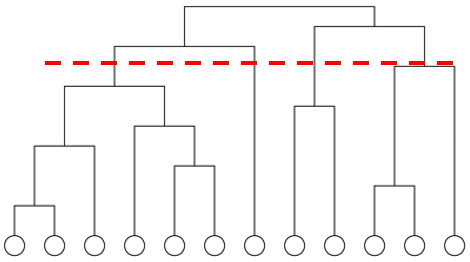
分层聚类

处理流程：

  • 计算所有节点对的距离
  • 从所有断开的n个节点开始
  • 为了减少权重，为节点对逐个添加边
  • 结果：递归分量，可在树的任一级切片

社交网络分析：社区结构

介数聚类

算法：

  • 计算所有边的介数
  • 当(任一边的介数大于阀值)：
    • 移除带有最高介数的边
    • 重新计算介数

介数在每一步都需要重新计算

  • 移除一个边会对其他边的介数造成影响
  • 代价昂贵：所有节点对最短路径– O(N3)
  • 可能需要重复N次
  • 即使使用最快的算法也无法扩大到几百个节点的网络

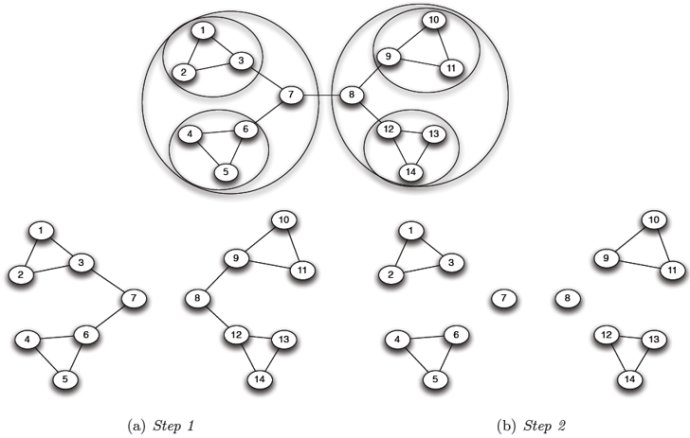
移除带有最高介数的边后，网络被分隔成分量。 社交网络分析：社区结构

模块度（Modularity）

考虑了社区内的边和社区与网络其他部分之间的边 模块度定义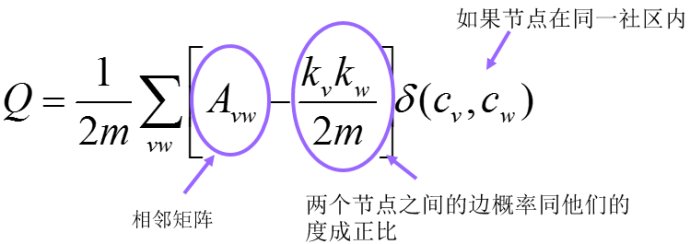： 社交网络分析：社区结构 假设有两个node v和w，它们的度数分别是Kv和Kw，那么如果随机的话，两个节点间有一条边的概率是(kv * kw)/2m。其中2m是所有节点的度数之和。 对于随机网络，Q=0。

算法：

  • 起始将所有节点当作鼓励的对待
  • 执行贪婪策略：
    • 一个接一个地连接带有模块度最大增长DQ的聚类
    • 当连接任意两个聚类时最大的DQ<=0时停止

参考

Cohesive Subgroups
Community Detection – Modularity的概念

第六讲：小世界网络

小世界网络

在网络理论中，小世界网络是一类特殊的复杂网络结构，在这种网络中大部份的节点彼此并不相连，但绝大部份节点之间经过少数几布就可到达。 在日常生活中，有时你会发现，某些你觉得与你隔得很“遥远”的人，其实与你“很近”。小世界网络就是对这种现象（也称为小世界现象）的数学描述。用数学中图论的语言来说，小世界网络就是一个由大量顶点构成的图，其中任意两点之间的平均路径长度比顶点数量小得多。除了社会人际网络以外，小世界网络的例子在生物学、物理学、计算机科学等领域也有出现。 二十世纪60年代，美国哈佛大学社会心理学家斯坦利·米尔格伦（StanleyMilgram）做了一个连锁信实验。他将一些信件交给自愿的参加者，要求他们通过自己的熟人将信传到信封上指明的收信人手里，他发现，20%的信件最终送到了目标人物手中。而在成功传递的信件中，平均只需要6.5次转发，就能够到达目标。也就是说，在社会网络中，任意两个人之间的“距离”是6。这就是所谓的“六度分隔”理论。

全局集聚系数(Global Clustering Coefficient)

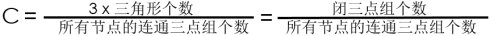
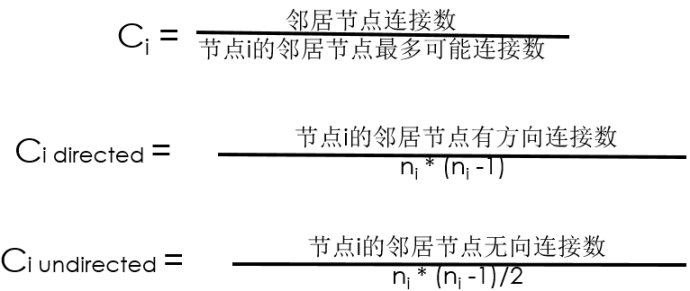
全局集聚系数基于节点的三点组。一个三点组由三个节点组成，其中可以两边连接(为闭三点组)或三边连接(开三点组)，统称连通三点组。 全局集聚系数是闭三点组个数(或三倍三角形个数)除以全部连通三点组个数。 该方法首次由Luce和Perry使用 (1949)。该指标指示了整个网络的集聚程度，可被用于无方向和有向网络。 定义： 社交网络分析：小世界网络

局部集聚系数(Local Clustering Coefficient, Watts&Strogatz1998)

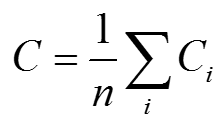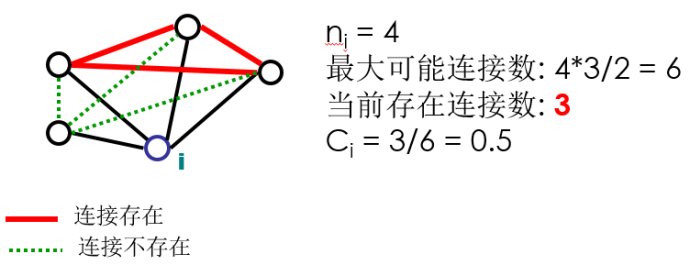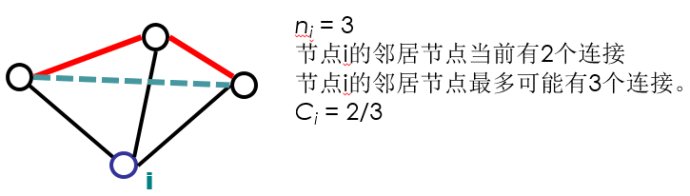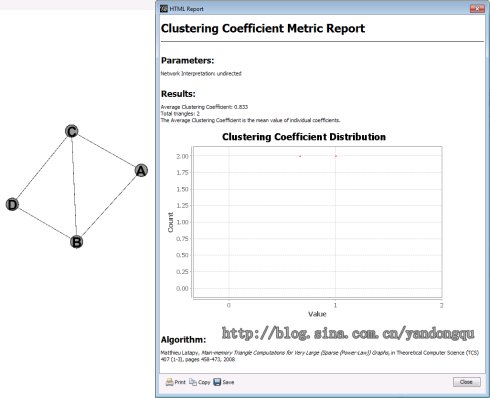
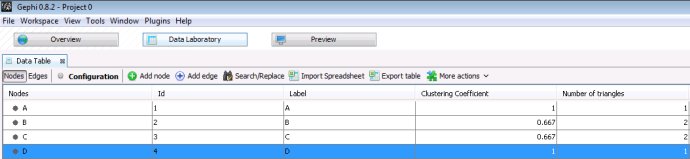对于每个节点i，ni是节点i的邻居节点个数。 社交网络分析：小世界网络 平均本地集聚系数： 社交网络分析：小世界网络 示例1： 社交网络分析：小世界网络 示例2： 社交网络分析：小世界网络 示例3： 我用Gephi做了一个例子，Gephi不计算全局集聚系数，它会计算平均集聚系数和每个节点的局部集聚系数。 社交网络分析：小世界网络 社交网络分析：小世界网络 平均集聚系数 = (1+0.667+0.667+1)/4 = 0.833，同软件所得一致。

下面手动算一下全局集聚系数： 闭三点组有6个： B->A<-C; A->B<-C; A->C<-B; C->B<-D;B->C<-D; B->D<-C 开三点组有2个： A->C<-D; A->B<-D 全局集聚系数=6/(6+2)=3/4=0.75

强联系(A strong tie)

  • 联系频繁
  • 亲密
  • 许多共同的联系人

连接边嵌入性(edge embeddeness)

嵌入性(embeddeness)：两个端点所共同拥有的邻居节点个数。 邻居节点重叠(neighborhood overlap)： 社交网络分析：小世界网络

分解局部结构：网络基序(Network motif)

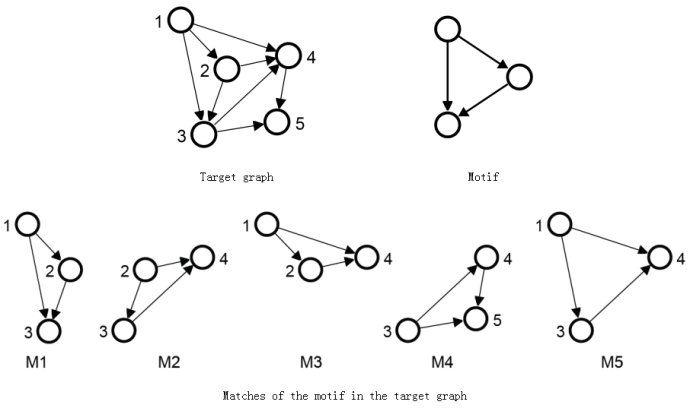
网络的复杂性本质上就是关系的复杂性。但是，研究者通过对真实网络的分析，发现各种关系种类的出现频率是非随机性的。某些特定的关系种类在网络中反复出现，形成网络的典型连接方式；不同类型的网络具有不同的典型连接方式。研究者把这些特定的关系种类称为“网络基序”，认为它们是一个网络的基本构造单元。 基序是从功能的角度来分析网络的构成，着眼于网络内各种成分之间连接的模式或关系。 社交网络分析：小世界网络

所有三节点基序

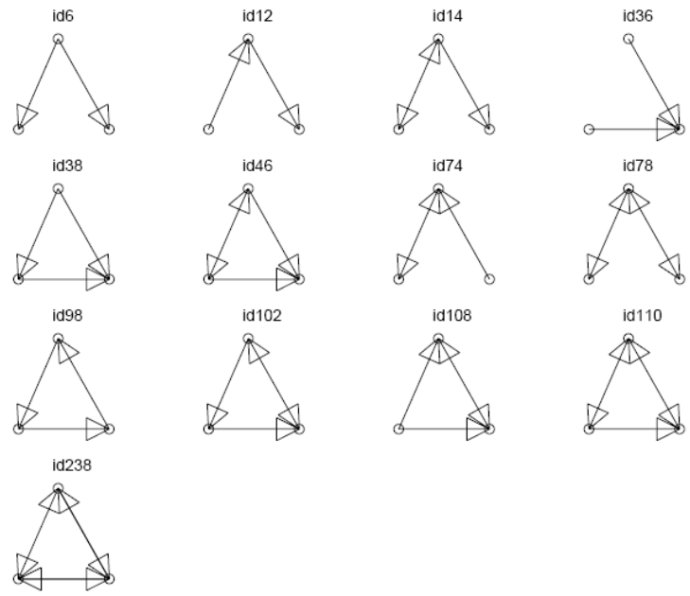
社交网络分析：小世界网络

网络基序示例(三节点)

社交网络分析：小世界网络

网络基序示例(四节点)

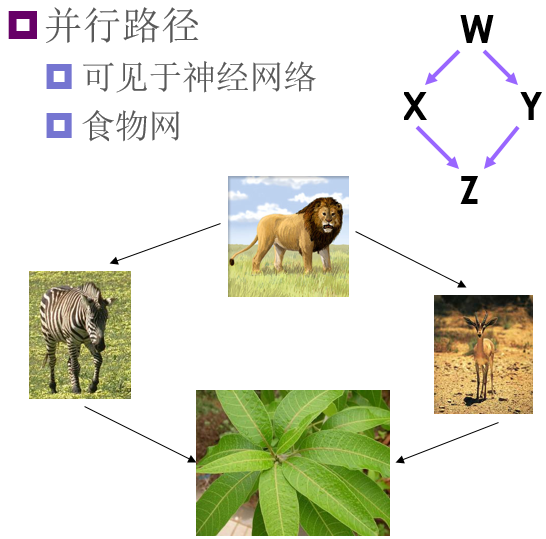
社交网络分析：小世界网络

真实网络与随机网络的网络基序对比

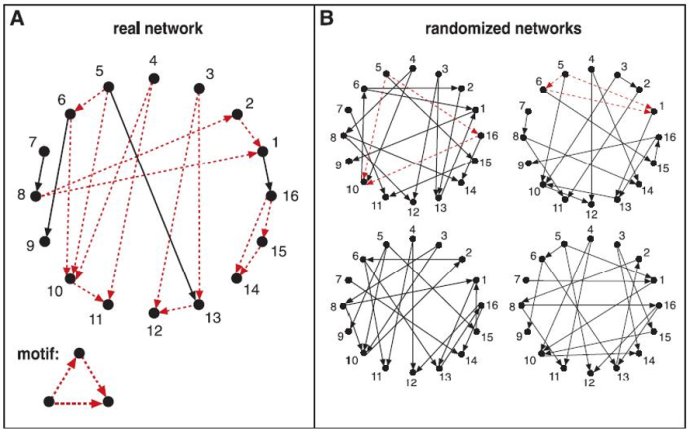
社交网络分析：小世界网络

网络基序探测

跟随机网络相比，一些网络基序更容易在真实网络中出现。

技术：

使用相同数量的节点和边构造随机网络(相同的节点度分布？) 计算图中的基序个数 计算Z-评分：给定基序个数偶然在真实网络出现的概率

基序软件

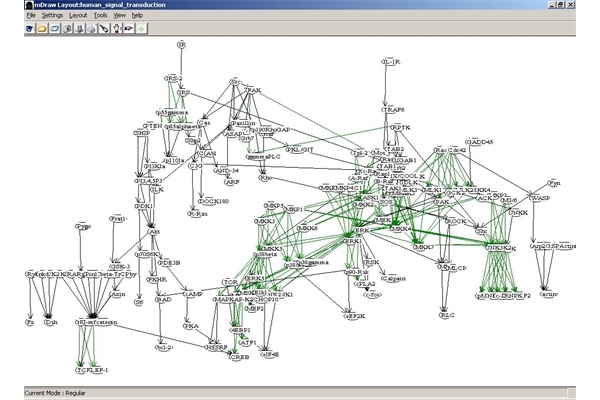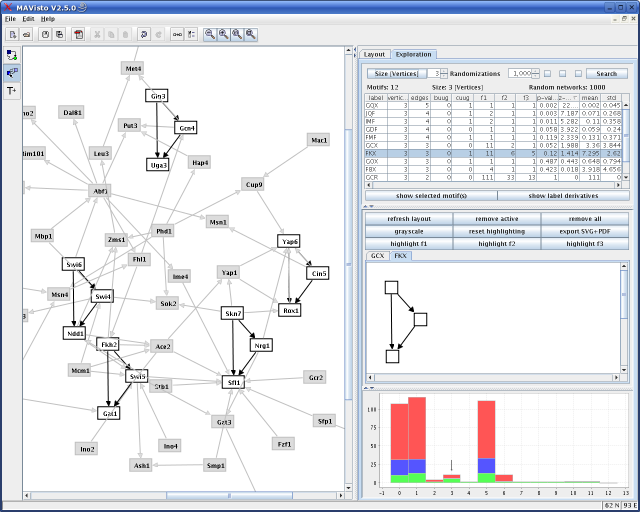
Uri AlonLab mfinder： 网络基序探测工具 Uri AlonLab mDraw： 网络基序可视化工具 社交网络分析：小世界网络 FANMOD：网络基序快速探测工具(开发者S. Wernicke和F. Rasche) 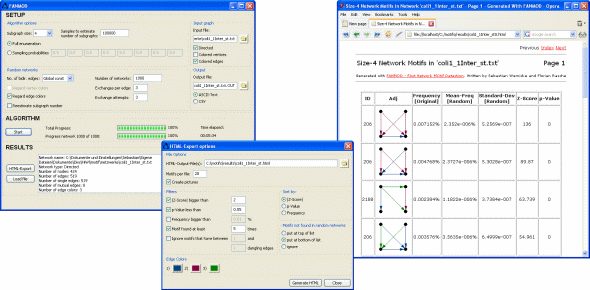社交网络分析：小世界网络 MAVisto：网络基序分析和可视化工具 社交网络分析：小世界网络

小网络现象

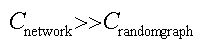
  • 高集聚系数         社交网络分析：小世界网络
  • 低平均最短路径长度 社交网络分析：小世界网络

例子： 秀丽隐杆线虫的神经网络 语言的语义网络 演员协作图 食物网

Watts/Strogatz模型：生成小世界图

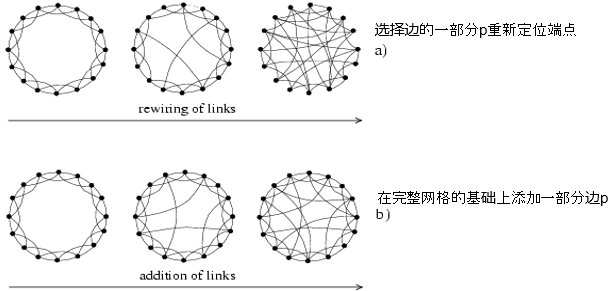社交网络分析：小世界网络 同许多网络生成算法一样：

  • 禁止自连接
  • 禁止多连接

示例：每个节点有K>=4最近邻居节点（局部） 可调：改变重连接给定边的概率p 小p：规则网格 大p：经典随机图 社交网络分析：小世界网络 通过数字模拟，将p从0增加到1：

  • 平均距离快速下降
  • 集聚系数缓慢增长

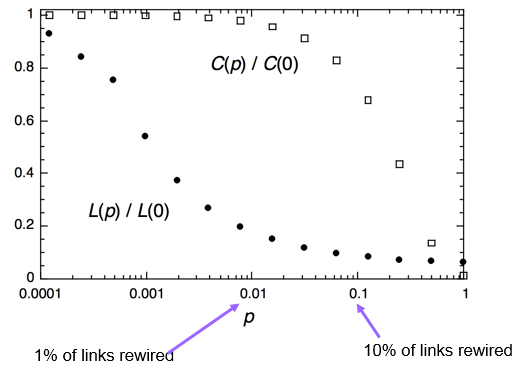
当重连接增加时的集聚系数和平均最短路径(ASP): 社交网络分析：小世界网络

WS模型集聚系数

连接的三点组重连接后仍然连接的概率：

  • 三个边没有一个重连接的概率(1-p)3
  • 边重连接回原有状态的概率很小，可以忽略

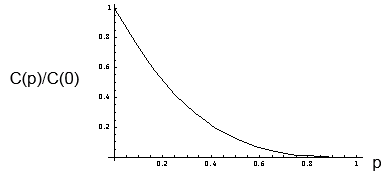
集聚系数= C(p) = C(p=0)*(1-p)3 社交网络分析：小世界网络

对比随机网络判断真实网络是否是“小世界网络”

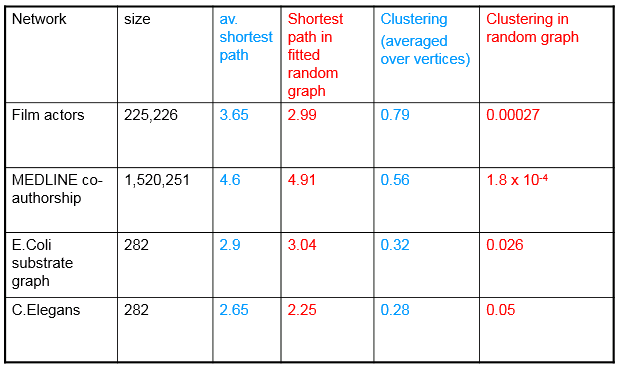
社交网络分析：小世界网络

WS模型：遗漏

  • 远程连接不可能同短程连接一样
  • 分层结构/组
  • 社交中心(hub)

Kleinberg的地理小世界模型

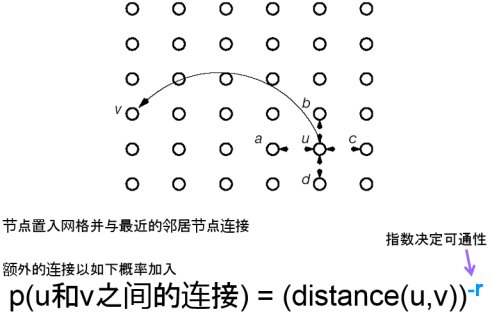
社交网络分析：小世界网络

可通性(Navigability)

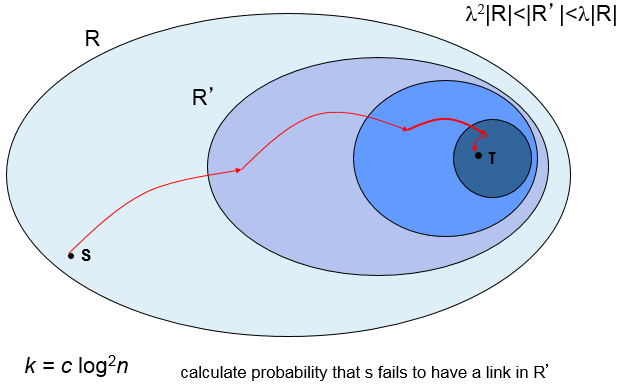
没看懂的说 社交网络分析：小世界网络

小世界的起源：群体关系

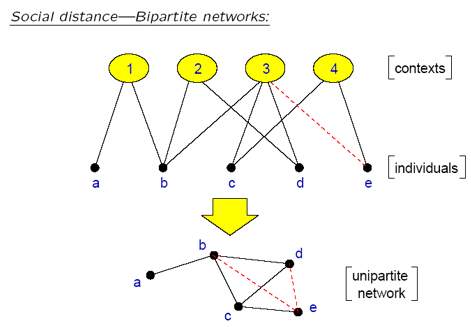
社交网络分析：小世界网络

分层小世界模型：Kleinberg

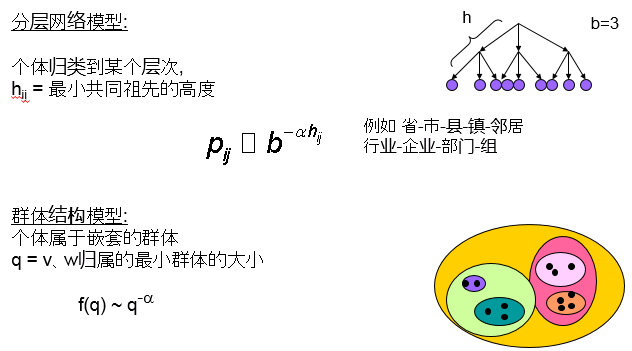
社交网络分析：小世界网络

分层小世界模型：WDN

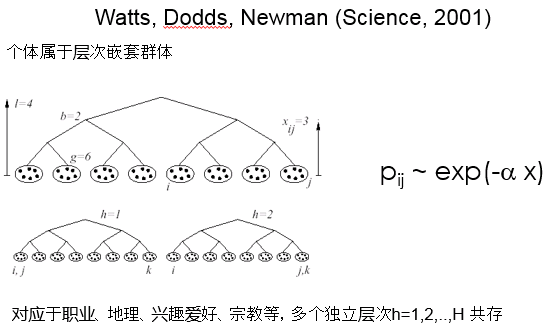
社交网络分析：小世界网络

生成小世界网络

  • 向节点分配属性(例如空间位置、组的成员关系等)
  • 根据一些规则添加或重连接边
    • 针对特定属性进行优化(模拟退火法)
    • 取决于已有节点、边（优先连接、链接复制）以一定概率添加边
    • 将节点模拟成代理决定是否添加或重连接边

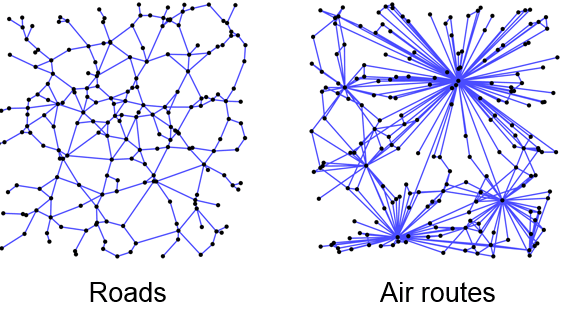
小世界起源：高效网络示例 连接与连通性之间的权衡

社交网络分析：小世界网络

优化的网络

社交网络分析：小世界网络

另一视图看优化的网络

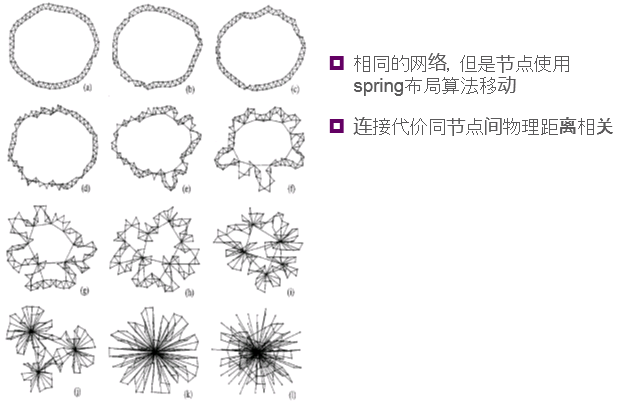
社交网络分析：小世界网络

从零开始优化

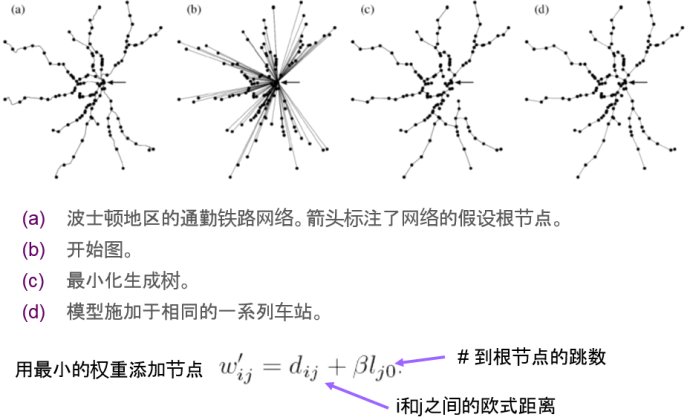
社交网络分析：小世界网络

引人深思

社交网络分析：小世界网络

参考

小世界网络
Clustering in Weighted Networks
Clustering coefficient
小世界网络模型
Social Network Analysis - 2012 - 001

数据集预处理及Gephi导入

紧赶慢赶忙完了社交网络分析课的编程大作业，选择的是经验性网络分析。 这次的大作业没有指定数据集，自己找数据集做分析。我在网上搜到以前一个同学做的移民分析，感觉很不错。然后，就茫然了。最怕这种自己找数据集的，以前有的课程介绍了一些比较好的开放数据集，可惜当时没觉得有什么太大的价值，没记呀！！！
费了半天，找了一个大不列颠的公路流量数据集，公路就是edge了，每个公路的两端就是node了，感觉还可以。数据集在线地址: http://data.dft.gov.uk/gb-traffic-matrix/Traffic-major-roads-miles.csv.数据集手册在线地址: http://data.dft.gov.uk/gb-traffic-matrix/all-traffic-data-metadata.pdf
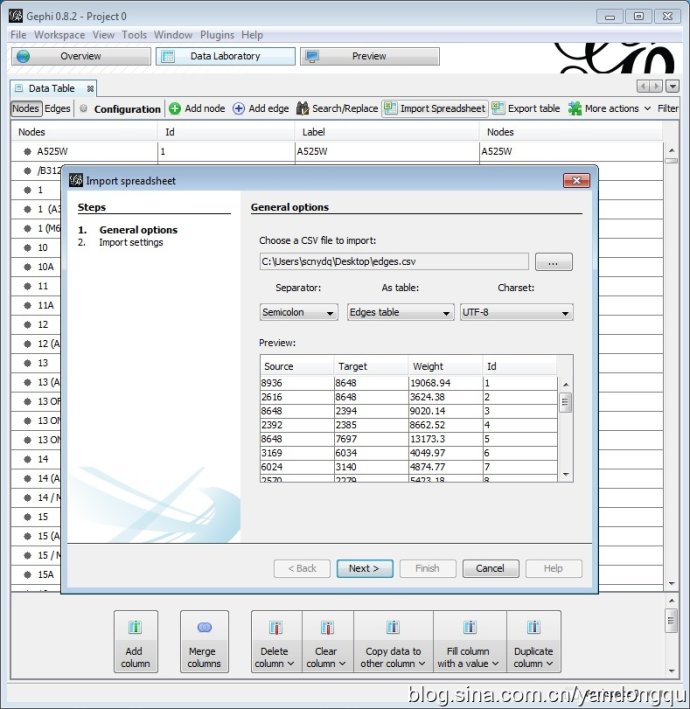
这次作业主要使用Gephi对数据集进行分析，所以我先使用R语言对原始数据集进行预处理，然后使用Gephi导入生成的nodes.csv和edges.csv。

if (!file.exists("./Traffic-major-roads-miles.csv")) {
    download.file("http://data.dft.gov.uk/gb-traffic-matrix/Traffic-major-roads-miles.csv", 
        destfile = "./Traffic-major-roads-miles.csv")
}
data <- read.csv("Traffic-major-roads-miles.csv", sep = ",")
data2013 <- subset(data, Year == 2013 & AllMV > 0, select = c(A.Junction, B.Junction, 
    AllMV))
data2013 <- data.frame(A.Junction = toupper(data2013$A.Junction), B.Junction = toupper(data2013$B.Junction), 
    Weight = data2013$AllMV, stringsAsFactors = FALSE)

A.junctions <- as.vector(data2013[, 1])
B.junctions <- as.vector(data2013[, 2])
junctions <- sort(unique(c(A.junctions, B.junctions)))

# write nodes.csv
nodes_print <- cbind(c("Nodes", junctions), c("Id", 1:length(junctions)), c("Label", 
    junctions))
nodes_print <- t(nodes_print)
write(nodes_print, file = "nodes.csv", ncolumns = 3, sep = ";")

# edges <- data.frame(Source=c('Source'), Target=c('Target'),
# Weight=c('Weight'), Id=c('Id')) for(i in 1:nrow(data2013)) { edges <-
# rbind(edges,
# data.frame(Source=as.character(which(junctions==data2013[i,1])),
# Target=as.character(which(junctions==data2013[i,2])),
# Weight=data2013[i,3], Id = as.character(i) ) ) }
edges <- data.frame(Source = c("Source", match(data2013[, 1], junctions)), Target = c("Target", 
    match(data2013[, 2], junctions)), Weight = c("Weight", data2013[, 3]), Id = c("Id", 
    1:nrow(data2013)), stringsAsFactors = FALSE)

# write edges.csv
edges_print <- as.matrix(edges)
edges_print <- t(edges_print)
write(edges_print, file = "edges.csv", ncolumns = 4, sep = ";")

代码里首先将所有公路起始和终止端点合并、去冗余、排序，用于生成nodes.csv。然后搜索每个公路端点在公路端点集合的下标，用于生成edges.csv。第一版的代码被迫使用了一次for循环，主要是只对which函数印象很深刻。在R语言里使用for循环慢的要死，感觉那是相当的屌丝。后来找到了match函数，感觉非常好。

社交网络分析课：数据集预处理及Gephi导入

0%