[JS] 图算法实践

最近需要用JavaScript处理图算法，没找到适合的库，就自己写一套玩玩。

Graph.js

仿照Graph.java写的，实现无向图API。

(function(){ 
  return Graph = (function () {
    // create empty Graph with V vertices
    function Graph(V) {
      this._V = V;
      this._E = 0;
      this._adj = [];
      for(var i=0;i<V;i++)
        this._adj.push([]);
    }

    Object.defineProperty(Graph.prototype, "V", {
      get: function () {
        return this._V;
      },
      enumerable: true,
      configurable: true
    });

    Object.defineProperty(Graph.prototype, "E", {
      get: function () {
        return this._E;
      },
      enumerable: true,
      configurable: true
    });

    // Adds the undirected edge v-w to this graph.
    Graph.prototype.addEdge = function (v, w) {
      this._E++;
      this._adj[v].push(w);
      this._adj[w].push(v);
    };

    // Returns the vertices adjacent to vertex v
    Graph.prototype.adj = function (v) {
      return this._adj[v];
    };

    return Graph;
  }());
})();

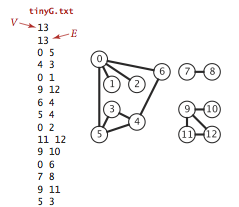
测试数据使用tinyG.txt，结果如下：

CC.js

仿照CC.java写的，使用DFS算法为无向图计算连通图。

(function(){ 
  return CC = (function () {

  // Computes the connected components of the DiGraph
  function CC(G) {
    this._marked = [];   // marked[v] = has vertex v been marked?
    this._id = [];     // id[v] = id of connected component containing v
    this._size = [];   // size[id] = number of vertices in given component
    this._count = 0;   // number of connected components
    for(var i=0;i<G.V;i++) {
    this._id.push(0);
    this._size.push(0);
    this._marked.push(false);
    }

    for(var v=0;v<G.V;v++) {
    if (!this._marked[v]) {
      this.dfs(G, v);
      this._count++;
    }
    }
  }

  // Returns the number of strong components.
  Object.defineProperty(CC.prototype, "count", {
    get: function () {
    return this._count;
    },
    enumerable: true,
    configurable: true
  });

  Object.defineProperty(CC.prototype, "ids", {
    get: function () {
    return this._id;
    },
    enumerable: true,
    configurable: true
  });

  // DFS on graph G
  CC.prototype.dfs = function (G, v) {
    this._marked[v] = true;
    this._id[v] = this._count;
    this._size[this._count]++;

    var adj = G.adj(v);
    for(var i=0;i<adj.length;i++) {
    var w = adj[i];
    if(!this._marked[w])
      this.dfs(G, w);
    }
  };

  // Are vertices v and w in the same connected component?
  CC.prototype.areConnected = function (v, w) {
    return this._id[v] === this._id[w];
  };

  // Returns the component id of the connected component containing vertex v
  CC.prototype.id = function (v) {
    return this._id[v];
  };

  // Returns the number of vertices in the connected component containing vertex v
  CC.prototype.size = function (v) {
    return this._size[v];
  };

  return CC;
  }());
})();

测试数据使用tinyG.txt，结果如下：

DiGraph.js

仿照Digraph.java写的，实现有向图API。

(function(){ 
  return DiGraph = (function () {
  // create empty digraph with V vertices
  function DiGraph(V) {
  this._V = V;
  this._E = 0;
  this._adj = [];
  for(var i=0;i<V;i++)
  this._adj.push([]);
  }

  Object.defineProperty(DiGraph.prototype, "V", {
  get: function () {
  return this._V;
  },
  enumerable: true,
  configurable: true
  });

  Object.defineProperty(DiGraph.prototype, "E", {
  get: function () {
  return this._E;
  },
  enumerable: true,
  configurable: true
  });

  // add edge v→w
  DiGraph.prototype.addEdge = function (v, w) {
  this._adj[v].unshift(w);
  this._E++;
  };

  // vertices pointing from v
  DiGraph.prototype.adj = function (v) {
  return this._adj[v];
  };

  DiGraph.prototype.reverse = function() {
  var reverse = new DiGraph(this._V);
  for (var v = 0; v < this._V; v++) {
  var adj = this.adj(v);
  for(var i=0;i<adj.length;i++) {
  var w = adj[i];
  reverse.addEdge(w, v);
  }
  }
  return reverse;
  };

  return DiGraph;
  }());
})();

测试数据使用tinyDAG.txt，结果如下：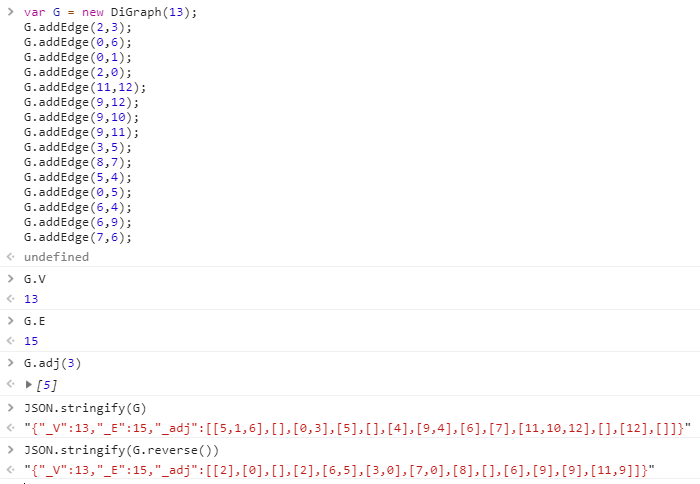

DepthFirstOrder.js

仿照DepthFirstOrder.java写的，为有向图计算前序和后序。

(function(){ 
  return DepthFirstOrder = (function () {

  // Determines a depth-first order for the DiGraph
  function DepthFirstOrder(G) {
  this._marked = [];   //marked[v] = has v been marked in dfs?
  this._pre = [];  // pre[v]  = preorder  number of v
  this._post = [];   // post[v]   = postorder number of v
  this._preorder = [];   // vertices in preorder
  this._postorder = [];  // vertices in postorder
  this._preCounter = 0;  // counter or preorder numbering
  this._postCounter = 0; // counter for postorder numbering
  for(var i=0;i<G.V;i++) {
  this._marked.push(false);
  this._pre.push(0);
  this._post.push(0);
  }

  for (var v = 0; v < G.V; v++) {
  if (!this._marked[v])
  this.dfs(G, v);
  }
  }

  // Returns the vertices in pre-order.
  Object.defineProperty(DepthFirstOrder.prototype, "preorder", {
  get: function () {
  return this._preorder;
  },
  enumerable: true,
  configurable: true
  });

  // Returns the vertices in post-order.
  Object.defineProperty(DepthFirstOrder.prototype, "postorder", {
  get: function () {
  return this._postorder;
  },
  enumerable: true,
  configurable: true
  });

  // Returns the vertices in reverse post-order.
  Object.defineProperty(DepthFirstOrder.prototype, "reversePost", {
  get: function () {
  return this._postorder.reverse();
  },
  enumerable: true,
  configurable: true
  });
  
  // Run DFS in digraph G from vertex v and compute pre-order/post-order
  DepthFirstOrder.prototype.dfs = function (G, v) {
  this._marked[v] = true;
  this._pre[v] = this._preCounter++;
  this._preorder.push(v);
  
  var adj = G.adj(v);
  for(var i=0;i<adj.length;i++) {
  var w = adj[i];
  if(!this._marked[w])
  this.dfs(G, w);
  }
  this._postorder.push(v);
  this._post[v] = this._postCounter++;  
  };
  
  // Returns the pre-order number of vertex
  DepthFirstOrder.prototype.pre = function (v) {
  return this._pre[v];
  };
  
  // Returns the post-order number of verte
  DepthFirstOrder.prototype.post = function (v) {
  return this._post[v];
  };
  
  return DepthFirstOrder;
  }());
})();

测试数据使用tinyDAG.txt，结果如下：

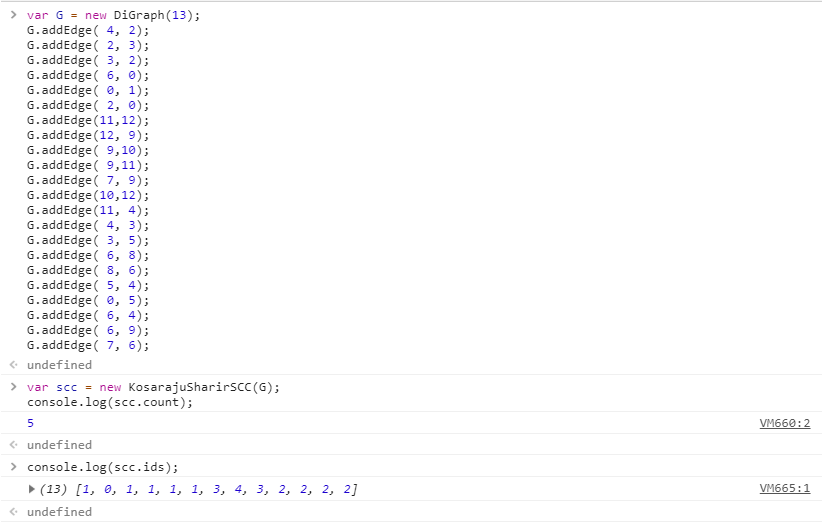
KosarajuSharirSCC.js

仿照KosarajuSharirSCC.java写的，使用Kosaraju-Sharir算法为有向图计算强连通图。

(function(){ 
  // Kosaraju-Sharir algorithm implementation to compute strong components in a DiGraph (with two DFSs).
  return KosarajuSharirSCC = (function () {

  // Computes the strong components of the DiGraph
  function KosarajuSharirSCC(G) {
  this._id = [];    // id[v] = id of connected component containing v
  this._marked = [];  // marked[v] = has vertex v been marked?
  this._count = 0;    // number of strong connected components
  for(var i=0;i<G.V;i++) {
  this._id.push(0);
  this._marked.push(false);
  }

  // compute reverse post-order of reverse graph
  var dfs = new DepthFirstOrder(G.reverse());
  var reversePost = dfs.reversePost;
  
  // run DFS on G, using reverse postorder to guide calculation
  for(var i=0;i<reversePost.length;i++) {
  var v = reversePost[i];
  if (!this._marked[v]) {
    this.dfs(G, v);
    this._count++;
  }
  }
  }

  // Returns the number of strong components.
  Object.defineProperty(KosarajuSharirSCC.prototype, "count", {
  get: function () {
  return this._count;
  },
  enumerable: true,
  configurable: true
  });

  Object.defineProperty(KosarajuSharirSCC.prototype, "ids", {
  get: function () {
  return this._id;
  },
  enumerable: true,
  configurable: true
  });

  // DFS on graph G
  KosarajuSharirSCC.prototype.dfs = function (G, v) {
  this._marked[v] = true;
  this._id[v] = this._count;

  var adj = G.adj(v);
  for(var i=0;i<adj.length;i++) {
  var w = adj[i];
  if(!this._marked[w])
    this.dfs(G, w);
  }
  };

  // Are vertices v and w in the same strong component?
  KosarajuSharirSCC.prototype.stronglyConnected = function (v, w) {
  return this._id[v] === this._id[w];
  };
  
  // Returns the component id of the strong component containing vertex v
  KosarajuSharirSCC.prototype.id = function (v) {
  return this._id[v];
  };

  return KosarajuSharirSCC;
  }());
})();

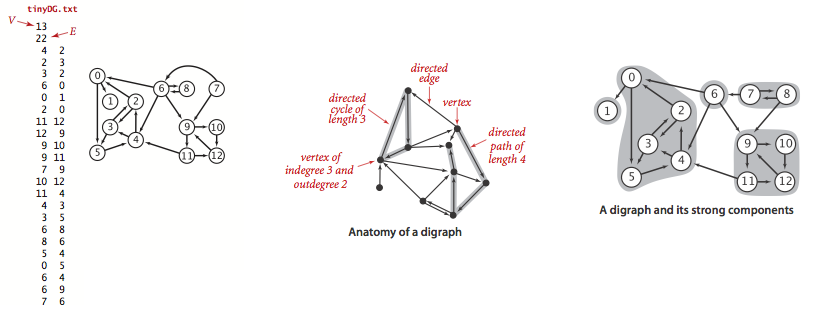
测试数据使用tinyDG.txt，结果如下：