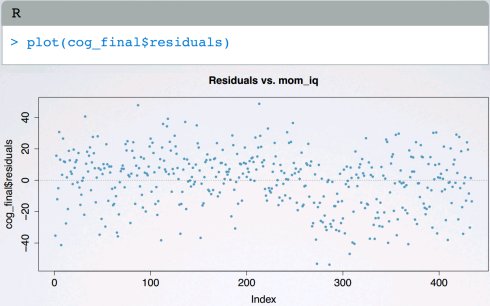
本文为Data Analysis and Statistical Inference学习笔记,课程地址为https://www.coursera.org/course/statistics。
介绍数据
数据基础
观察值、变量、数据矩阵数据类型:
- 数字变量:分为连续的和离散的
- 分类变量:分为有序(ordinal)的和普通无序的变量关系:
- 关联Assocaited (Dependent):分为正的和负的
- 独立Independent
研究方法
- 观察性研究Observational Study:直接取现实中的数据,探究变量间的相关性
- retrospective:依赖以前的数据
- prospective:在研究中收集新的数据
- 实验性研究Experiment: 随机分配对象到实验组;建立因果性连接观察性研究和实验性研究主要区别在于是否人为地施加了干预措施
观察性研究和抽样策略
为什么抽样?
- 某些个体很难定位和测量;
- 统计总体很少保持不变抽样偏差源
- 便利样本Convenience sample:更易于被访问到的用户更可能被包含到采样中
- 无响应样本Non-response:仅部分被随机采样的被访者填写了调查问卷,这样的采样无法代表统计总体
- 自发性响应样本Voluntary response:对调查问卷中的问题更感兴趣的人积极主动填写调查问卷抽样方法
- 简单随机抽样Simple random sample (SRS):不做控制随机地取样
- 分层抽样Stratified sample:对人群做分析,按相似性分成若干的阶层,在各阶层内取样
- 整群抽样cluster sample:随机将统计总体分成若干群,随机取一些群,再在这些群内取样混杂变量 Confounding/lurkvariable:对解释变量和响应变量都有影响的额外变量,使解释变量和响应变量看起来有关系
实验性研究
设计原则
- control:比较实验组与对照组
- randomize:保证对象在两个组分配的随机性
- replicate:足够大的实验量或整个实验可复制
- block:消除已知或可疑变量对输出的影响。例子:设计实验研究是否能量胶囊有助于奔跑更快: 实验组treatment:能量胶囊 对照组control:无能量胶囊能量胶囊可能对专业运动员和业余运动员影响不同消除专业状态: 将样本拆分为专业运动员和业余运动员 将专业运动员和业余运动员随机平均分配到实验组和对照组消除变量和解释变量的区别:
- 解释变量(factors):施加于实验个体的条件
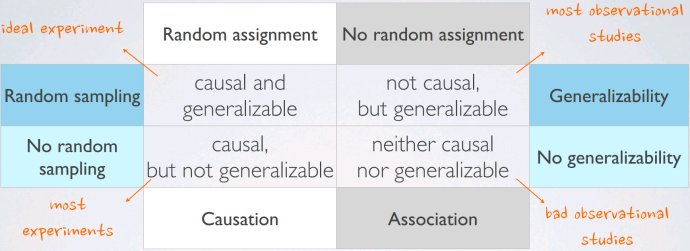
- 消除变量:我们需要控制的实验个体自带特征消除与分层很相似,区别在于:
- 在随机分配过程中消除,用于取得因果性
- 在随机抽样过程中分层,用于概化generalizability
术语
- 安慰剂:假处理,经常在药物研究中用作对照组
- 安慰剂效应:展示使用安慰剂的变化
- 盲 :实验个体不知道其所在组
- 双盲:实验个体和研究者都不知道其所在组在需要从人的主观感受中剥离客观结论的社会性研究(比如药物实验)中,如果被试的主观感受会影响数据结果,就需要给予对照组无实质作用的安慰剂,并且对其隐藏其属于实验组还是对照组的信息,以区分实验组的变化和安慰剂效应,这就叫blindexperiment;更进一步,如果研究者的主观感受也会影响实验结果,则对研究者也隐藏实验与对照的分组信息,这就是通常说的双盲实验
随机抽样和随机分配
数值型数据的可视化
散点图scatterplot
可以从中归纳两个变量的相关性。相关性有几个性质:正/负相关、形状(线性、非线性)、强/弱相关,异常值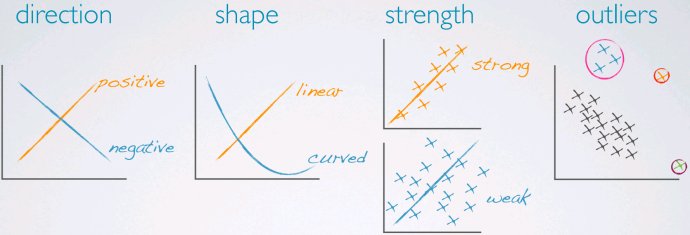
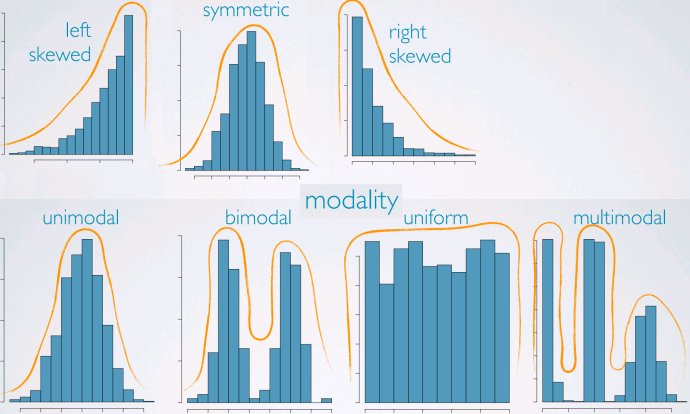
直方图histogram
可以给出一个数据密度的视图,并且可以观察:
- 偏度:描述了数据密度的左右分布,左偏/右偏/对称
- 形态(modality):正态分布/均匀分布/双峰分布/多峰分布等等
- 区间划分不能过宽或过窄
点阵图dotplot
当研究个体值时有用,样本量太大时不太适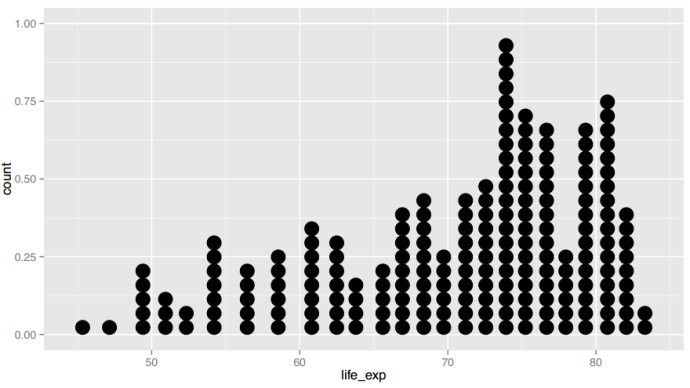
箱形图boxplot
在强调异常点、中位数、四分位距(Interquartile range,IQR,即Q3-Q1)时有用。
强度图intensity map
用于空间分布。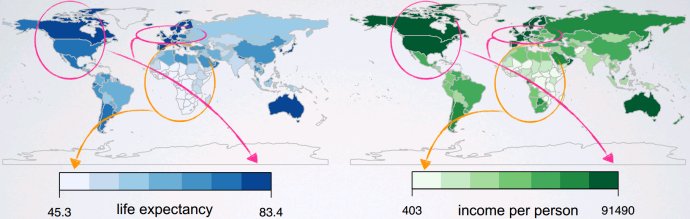
中心测量
均值mean、中位数median、众数mode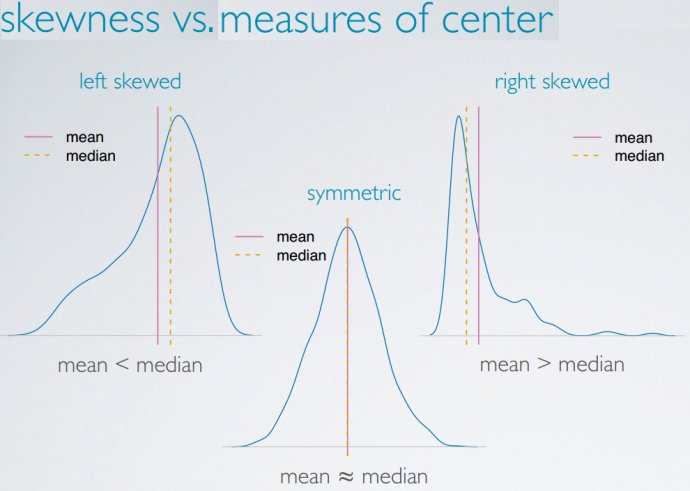
分布性测量
- 范围range:最大值-最小值
- 方差variance:
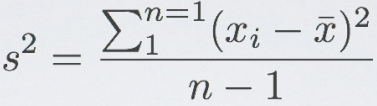
- 标准差standard deviation:
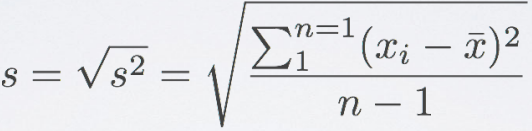
- 四分位距Interquartile range:
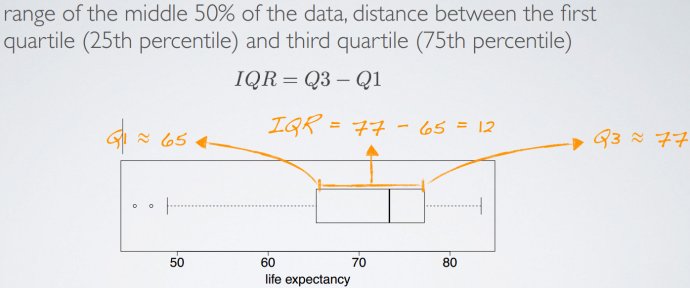
健壮统计量
用于测评特异值是否作用较小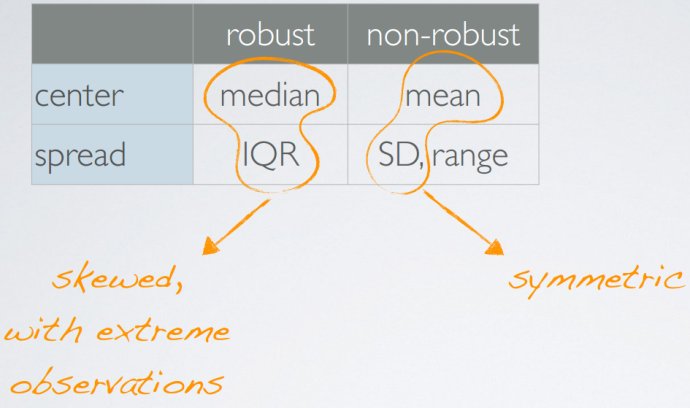
数据转换:
通过函数对数据进行尺度变换,用于换一种数据观察角度;降低偏度;非线性转换为线性。示例为对数转换、平方根转换、倒数转换。1. 对X轴和Y轴都做变换;2. 保持X轴不变,对Y轴做变换。
观察类别变量
- 单个类别变量
- 频率表和条形图barplot
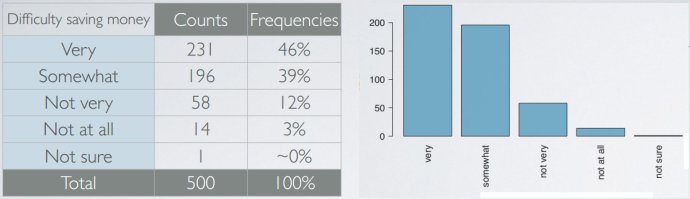 条形图和直方图区别:条形图用于类别变量,直方图用于数值变量;直方图的X轴表示的是数值,并且数序不可更换。
条形图和直方图区别:条形图用于类别变量,直方图用于数值变量;直方图的X轴表示的是数值,并且数序不可更换。 - 饼图 pie chart:分类较多时不建议使用。
- 频率表和条形图barplot
- 两个类别变量
- 相依表contingency table
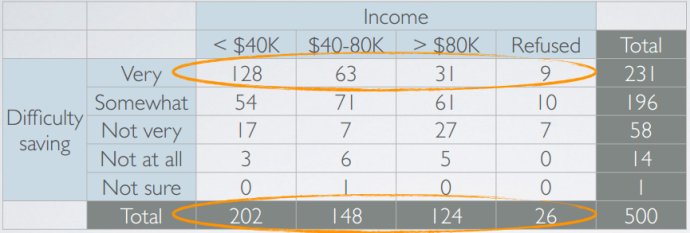
- 分段条形图segmented barplot
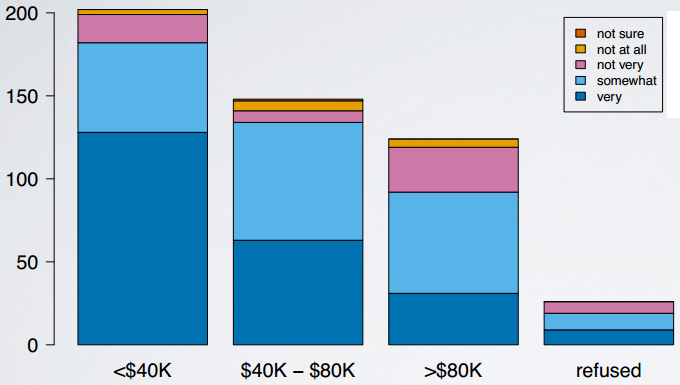
- 马赛克图mosaicplot
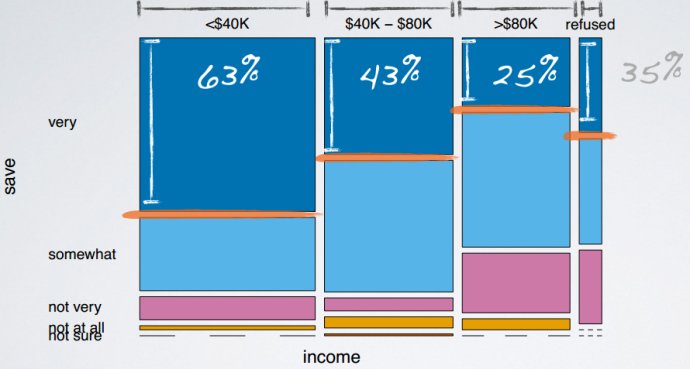
- 相依表contingency table
- 一个类别变量和一个数值变量并排箱体图side-by-side boxplot
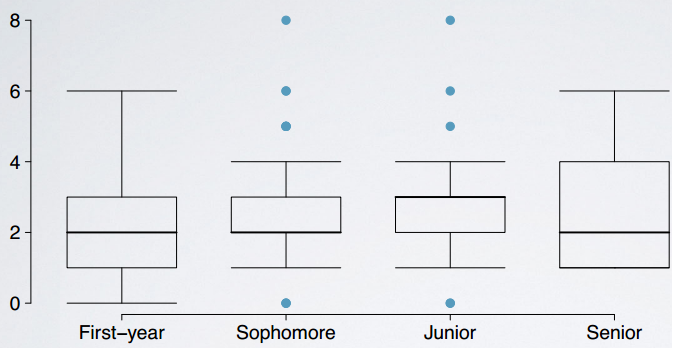
推断介绍
推断框架:
- 设置代表现状的虚假设(null hypothesis, H0)。
- 设置代表所研究问题的备择假设(alternative hypothesis, HA)。
- 假定虚假设为真,通过模拟或理论方法进行假设检验。
- 如果结果表明数据没有提供支持备择假设的证据,坚持虚假设;否则,拒绝虚假设,采用备选假设。模拟方法进行假设检验:
- 设置虚假设和备择假设
- 假定虚假设为真,进行模拟实验
- 评估观测结果比原数据观察到的异常值一样多或更多的概率(p-value)
- 如果概率低,则拒绝虚假设,采用备选假设。
概率分布
概率规则
- 事件A或B发生概率: P(A or B) = P(A) + P(B) - P(A and B)
- 事件A和B同时发生概率: P(A and B) = P(A|B) x P(B)
- 条件概率:P(A|B) = P(A and B) / P(B)
- 不相交事件(disjoint, mutually exclusive):事件A和B不会同时发生 p(A and B)=0,p(A or B)=p(A)+p(B), p(A|B)=0
- 互补事件(complementary):概率和为1的不相交事件 p(A and B)=0, p(A|B)=0, p(A orB)=1, p(A)+p(B)=1
- 独立事件(independent):事件A是否发生对事件B没有影响 p(A|B)=p(A), p(A andB)=p(A)p(B)
概率分布
列出样本空间所有输出及其概率
概率树
按照多个变量层层写出条件概率

贝叶斯推断
利用先验信息,例如以前发布的研究成果或物理模型当收集数据时自然集成,并更新先验信息避免反直觉的p-value定义:P(observed or more extreme outcome | H0 istrue)而是基于后验概率做判决:P(hypothesis is true | observed data)好的先验信息有帮助,坏的先验信息有损害。但是先验信息跟能收集到更多数据相比不重要。更高级的贝叶斯技术提供了频率模型无法表示的灵活度 过程:
- 设定先验信息
- 收集数据
- 获得后验信息
- 使用后验信息更新先验信息
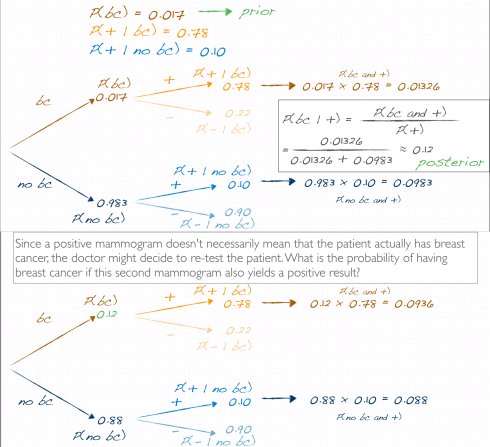 贝叶斯检验是一个迭代过程,课程中以疾病诊断为例探讨了这一过程。根据经典的概率错觉,对于发病率很低的疾病,即使诊断本身作用在发病人群中正确率很高,在整个人群上作用时也会极差,那么这时候针对第一次诊断阳性的人群再迭代进行贝叶斯概率的计算,由于初始条件改变,正确率就能提高了
贝叶斯检验是一个迭代过程,课程中以疾病诊断为例探讨了这一过程。根据经典的概率错觉,对于发病率很低的疾病,即使诊断本身作用在发病人群中正确率很高,在整个人群上作用时也会极差,那么这时候针对第一次诊断阳性的人群再迭代进行贝叶斯概率的计算,由于初始条件改变,正确率就能提高了
正态分布
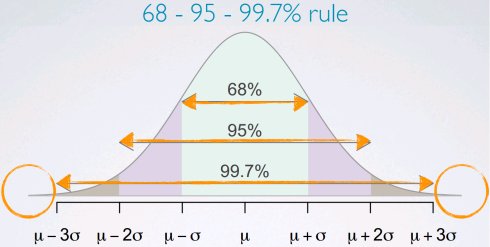
> 1-2*pnorm(1, mean = 0, sd = 1, lower.tail = FALSE)
[1] 0.6826895
> 1-2*pnorm(2, mean = 0, sd = 1, lower.tail = FALSE)
[1] 0.9544997
> 1-2*pnorm(3, mean = 0, sd = 1, lower.tail = FALSE)
[1] 0.9973002
标准差计分法 standardized (Z) score:观察值落在平均值之上或之下标准差的个数
Z = (observation - mean)/SD
异常观察值: |Z| > 2
百分位数percentiles:观察值落在低于某个数据点的百分比
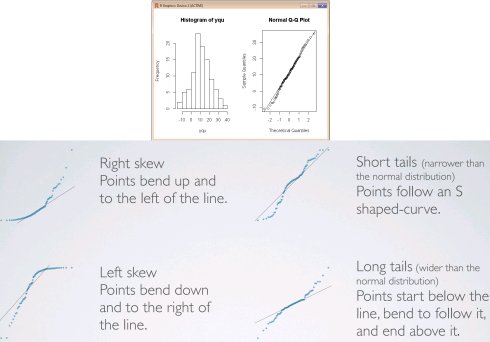
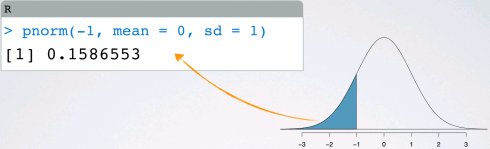 正态概率图(normal probability plot): Y轴数据值,X轴正态分布的理论分位数
正态概率图(normal probability plot): Y轴数据值,X轴正态分布的理论分位数
par(mfrow=c(1,2))
yqu <- rnorm(100, mean=10, sd=10)
hist(yqu)
qqnorm(yqu); qqline(yqu)
二项分布
伯努利随机变量(Bernoulli random variable):单个实验仅有两种可能输出
二项分布(binomial distribution):描述n个独立的成功概率为p的伯努利实验获得k次成功的概率R函数:dbinom 二项分布条件:
二项分布条件:
- 实验必须独立
- 实验次数n必须固定
- 每次实验输出必须分类为成功或失败
- 每次实验的成功概率p必须相同

大数极限定理与假设检验
采样可变性
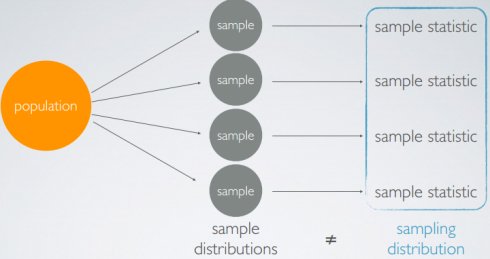
中心极限定理
样本统计分布趋向于正态分布,其均值接近总体均值,标准差为原总体标准差除以样本量的平方根CLT条件:
- 独立:样本观察值必须独立
- 随机抽样/分配
- 对于无放回抽样,样本个数n必须小于总体的10%,太大以后样本中的数据很难相互独立
- 样本大小/偏斜度:或者总体分布是正态分布,或者总体分布是偏斜的但样本很大(经验法则:n>30)
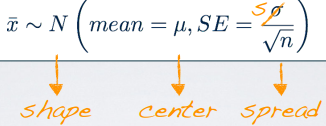
置信区间(confidence interval)
总体参数值的可能范围置信区间=点估计±误差幅度(误差边际,margin of error)

总体均值的置信区间
z*: 90% 1.65
95% 1.96
98% 2.33
99% 2.58
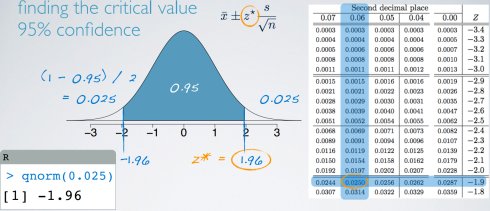 置信区间增大,宽度增大,准确度变大,精确度变小。唯有增加样本大小,可以获得高准确度和高精确度。
置信区间增大,宽度增大,准确度变大,精确度变小。唯有增加样本大小,可以获得高准确度和高精确度。
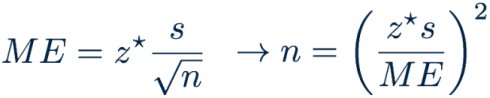
假设检验
- 基于置信区间的假设检验:判断现状是否存在于置信区间内
- 基于p-value的假设检验:p-value = P(observed or more extreme outcome | H0 true)使用测试统计计算p-value,虚假设为真的情况下当前数据集倾向备择假设的概率。如果p-value低(低于显著水平α,通常为5%),如果虚假设为真的情况下很难观测到(样本这样的)数据,因此拒绝H0。如果p-value高(高于α),即使虚假设为真也能观测到(样本这样的)数据,因此不拒绝H0。

- 双边检验(two-sided test):置信区间两边都纳入考虑单边与双边检验,p-value的定义相同,但计算方式有不同
决策失误:
- 第一类错误(Type 1 error)是当H0为真时拒绝H0 – 错杀好人。
- 第二类错误(Type 2 error)是当HA为真时拒绝H0失败 – 错放坏人。
P(Type 1 error | H0 true) = α,显著性水平(significance level,α)越高,犯第一类错误的可能性越大。 如果第一类错误代价高,选择小的显著水平(例如0.01);如果第二类错误代价高,选择高的显著水平(例如0.10) 第二类错误发生概率β计算不太直接,但是它取决于效应值(effect size, δ), 点估计与nullvalue之间的差。
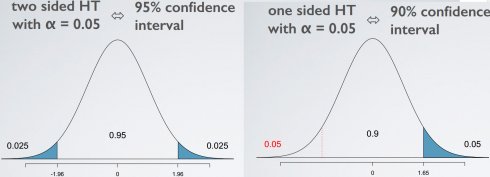
置信区间与假设检验的约定
带有门限值α双侧假设检验等同于置信区间CL = 1 - α
带有门限值α单侧假设检验等同于置信区间CL = 1 - (2 x α)
statistical vs. practical significance
点估计和null value之间的真实差异更容易在大样本情况下检测到。
然而,太大的样本会导致很小的效应值(样本均值-null value)获得很大的统计显著性,即使其实际并不显著。

数字变量推断
两组数据比较
成对数据

独立数据

bootstrapping
bootstrapping术语取自短句“pulling oneself up by one’sbootstraps”,暗指没有外力的情况下完成不可能实现的任务。统计中指使用给定样本中的数据估计总体参数。
- 获得bootstrap样本 - 使用原样本有放回抽样获得相同大小的随机样本
- 计算bootstrap统计量 - 通过bootstrap样本获得平均值、中值、概率等统计量
- 多次重复步骤1和2以创建bootstrap分布 - bootstrap统计量的分布
估计方法:
- 百分比方法:通过排除两端的数据,直接取bootstrap分布中间的95%
- 标准差方法:先计算bootstrap分布的均值与标准差,再计算95%区间
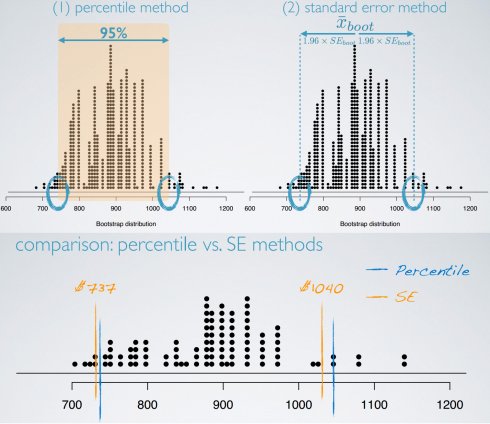
限制: 没有类似于中心极限定理时的严格条件 如果bootstrap分布特别倾斜或稀疏,则可信度低需要一个可以概化的代表性样本。 若原样本有偏,则bootstrap结果很可能有偏
bootstrap vs. 抽样分布
抽样分布使用总体进行有放回抽样 Bootstrap分布使用样本进行有放回抽样 两者都是样本统计分布
t分布
当n比较小且方差σ未知,使用t分布解决标准差估计的不确定性。 t分布有一个参数:自由度(degrees of freedom, df),决定分布尾部的厚度。自由度越大,越接近正态分布。 t统计用于推断σ未知且n < 30时的均值
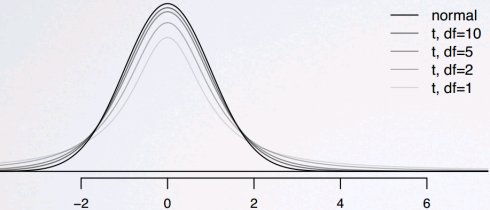
基于小样本估计均值
R函数实例:
qt(0.025, df = 21)
pt(2.30, df = 21, lower.tail = FALSE)

基于小样本比较均值

多均值比较
当比较两组均值时可以使用Z或T检验,当比较3+组均值时需要使用方差分析(analysis ofvariance,ANOVA)和F检验。

总平方和(sum of squares total, SST)
估量响应变量的总可变性,跟方差计算相似(除了不除以样本数)

组平方和(sum of squares groups, SSG)
估量组间可变性,可解释的可变性:组均值与总均值之间样本数加权的偏差
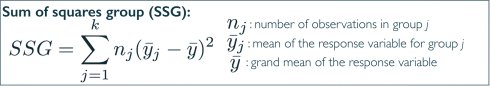
误差平方和(sum of squares error, SSE)
估量组内可变性,不可解释的可变性:组变量由于其他原因无法解释

自由度
总自由度:总样本量减一组自由度:组样本量减一误差自由度:前两者相减

平均平方和

F统计
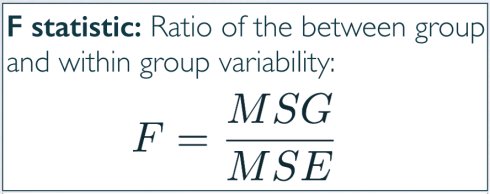
p-value计算
pf(21.735, 3, 791, lower.tail = FALSE)
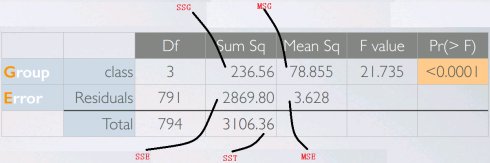
ANOVA条件
(1)独立性:抽样的观察值必须彼此独立,总是很重要,但有时很难检查随机样本/分配每组样本数小于总体的10%仔细思考组是否独立(例如,没有配对) (2)近似正态分布:当样本小时尤为重要每组内的响应变量分布必须近似正态分布 (3)恒定的方差:当每组样本个数变化大时尤为重要组之间的可变性必须一致:homoscedastic groups! 数据分析与统计推断:数字变量推断
多次比值
ANOVA可以判别多组均值是否相等,如果不相等,那如何判别每组均值是否相等? 对可能的每两组进行t检验 多次检验将导致膨胀的第一类错误率 解决方案:使用修改过的显著水平
Bonferroni correction建议更严厉的显著水平更适合这类检验。


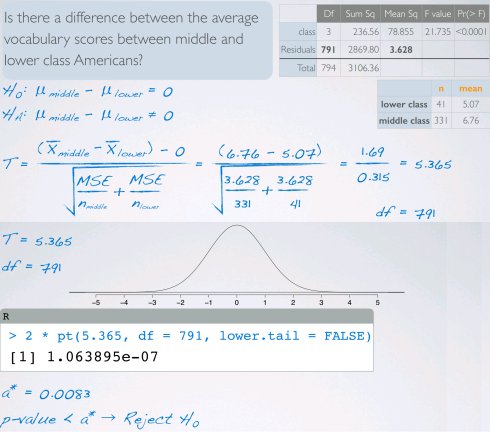
分类变量推断
抽样可变性
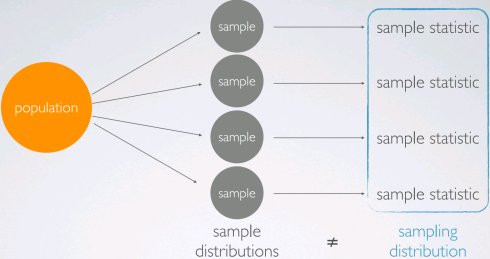
用于概率的大树极限定理

概率的置信区间

计算符合误差幅度的样本个数

概率的假设检验

两个概率差的置信区间

两个概率差的假设检验

小样本概率 & 比较两个小样本概率
模拟方法进行假设检验:
- 假设检验的最终目标是p-value,P(observed or more extreme outcome | H0true)
- 假定虚假设为真,设计模拟方法
- 多次重复模拟,记录相关样本统计量
- 计算倾向备选假设的模拟概率作为p-value。
卡方拟合度检验(chi-square GOF test)
拟合度(goodness of fit)检验:评估观察数据有多拟合期望分布单个类别变量,变量值大于2级
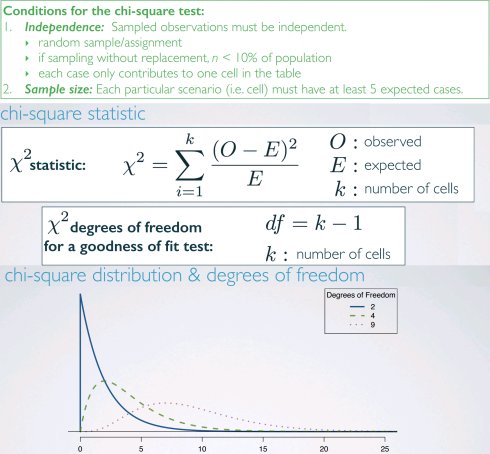
卡方检验的p-value
用于卡方检验的p-value定义为高于计算的检验统计量的尾部区域由于检验统计量总是正数,更高的检验统计量意味着与虚假设偏离更大。
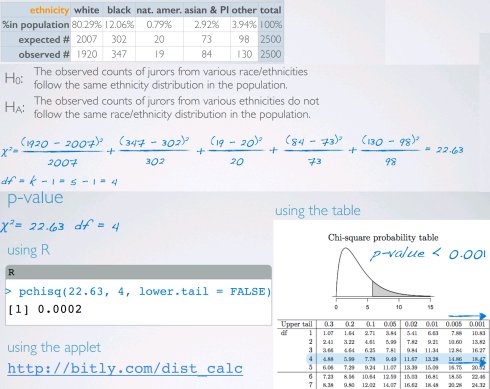
卡方独立检验
独立检验:评估两个类别变量之间的关系两个类别变量,类别值大于两级

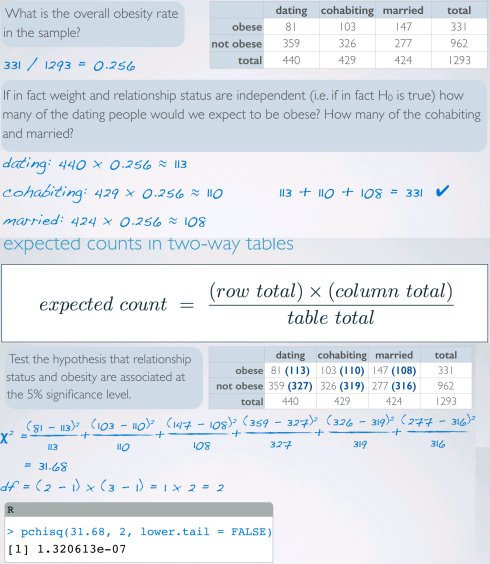
线性回归
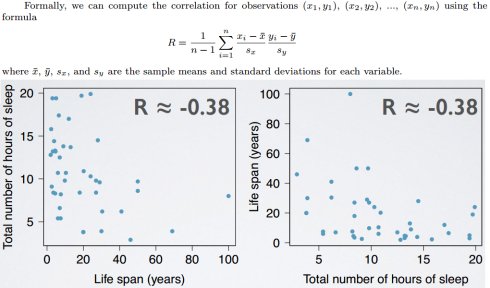
相关性(correlation)
相关性描述了两个变量之间线性关联的强度,表示符号为R。属性:
- 相关系数的幅度(绝对值)测量两个数字变量之间线性关联的强度
- 相关系数的正负指示关联的方向
- 相关系数总是介于-1(完美负线性关联)和1(完美正线性关联)之间,R=0指示没有线性关系
- 相关系数没有单位,不受变量中心点和比例变化的影响
- X与Y的相关性等同于Y与X的相关性
- 相关系数对异常点敏感
残差(residuals)
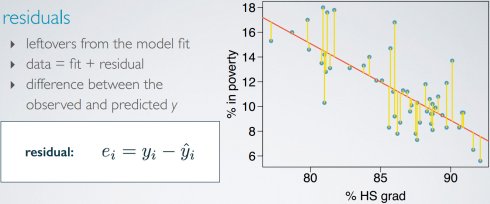
测量线性匹配度
方案1:最小化残差的幅度和
方案2:最小化残差平方和。更常使用,易于计算,残差增幅更大。

使用线性模型对解释变量给定值预测响应变量值称之为预测(prediction)。
使用模型估计原有数据域外的值称之为外推法(extrapolation)。优势预测可能是外推法。
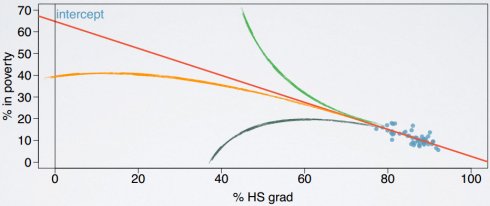
线性回归条件
(1)线性
解释变量和响应变量值间的关系必须是线性的;
存在匹配非线性关系模型的方法;
使用数据散点图scatterplot或残差图residuals plot检查
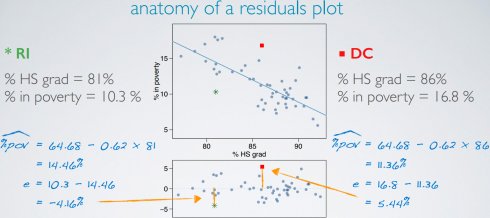
(2)近似正态残差
残差必须近似正态分布,中心点为0;如果有异常观察值不遵循正常数据的趋势,有可能不满足该条件使用残差的直方图或正态概率图检查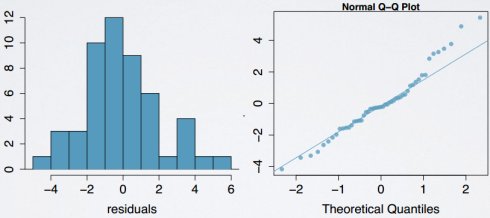
(3)恒定可变性
点围绕最小平方和线(the least squaresline)的可变性应该大概恒定,暗指残差围绕0的可变性应该大概恒定,这也称为同方差性(homoscedasticity)。
使用残差图residuals plot检查
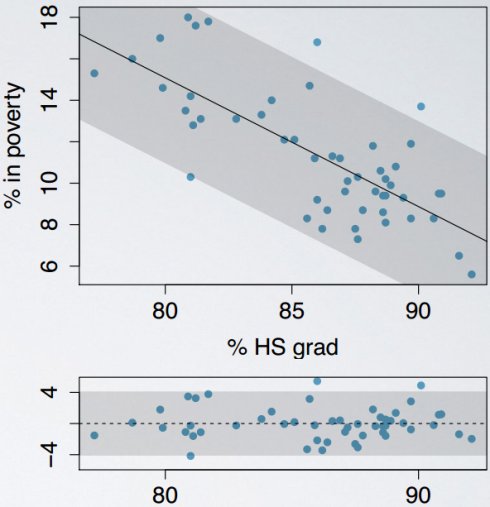
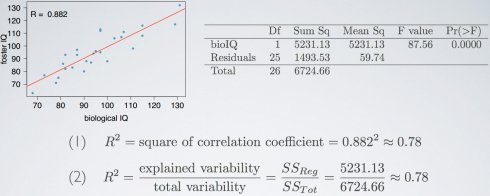
R squared
评估线性模型拟合度更常使用,通过相关系数平方计算而得; 可以获知线性模型解释响应变量可变性的百分比,剩余可变性无法由模型解释; 介于0和1之间。
使用分类解释变量的回归

异常点类型
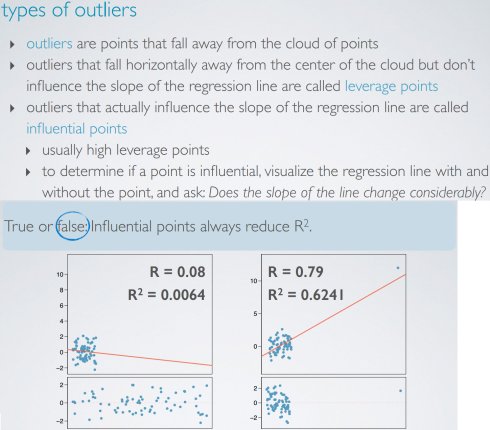
线性回归推断
由于我们经常检查解释变量和响应变量之间是否存在关系,对斜率虚假设值经常为0;很少对截距进行推断。
对线性回归的每个估计参数都会损失一个自由度。
我们必须了解所工作的数据:随机样本、非随机样本或总体。如果已有总体数据,假设推断及其p-value结果就毫无意义。如果样本是非随机(有偏)的,结果将不可信。
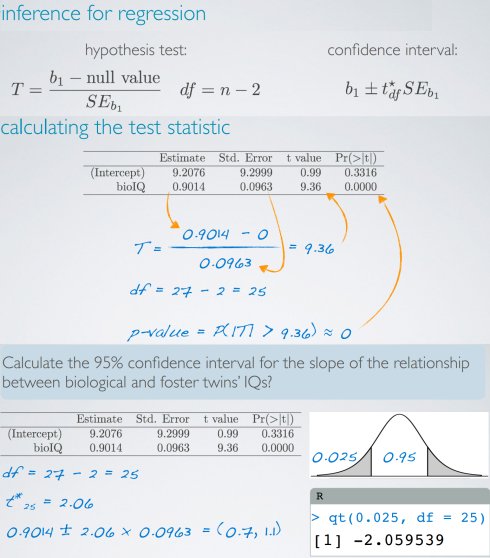
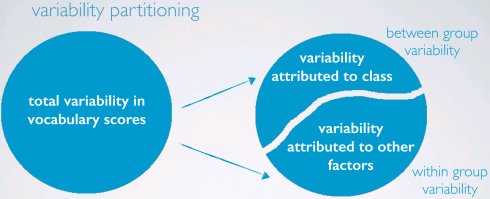
变异分解(variability partitioning)
t检验是评估x和y线性关系斜率假设检验的证据力度的一种方式。将y可变性分解为可解释和无法解释的可变性,需要使用方差分析ANOVA。

再学习 R sqared
Rsqared是模型可以解释y可变性的比例。很大,即x和y之间存在线性关系;小,则x和y之间存在线性关系的证据不令人信服。
两种结算方式:相关性,相关系数平方;定义,总可变性中可解释可变性的比例。
多元线性回归
adjusted R squared

共线性(collinearity):当两个预测变量彼此相关就可以说共线的。预测变量也称为独立变量,因此它们应该彼此独立。引入共线的预测变量(多重共线性,multicollinearity)使模型估计更加复杂。 简约法(parsimony):避免添加互相关联的预测变量,因为这些变量不会带来新信息;优选最简单最好的模型,例如精简模型;加入共线的变量会导致回归参数有偏估计;当无法避免观察数据中的共线性,经常设计实验来控制关联的预测变量。
多元线性回归推断

模型选择
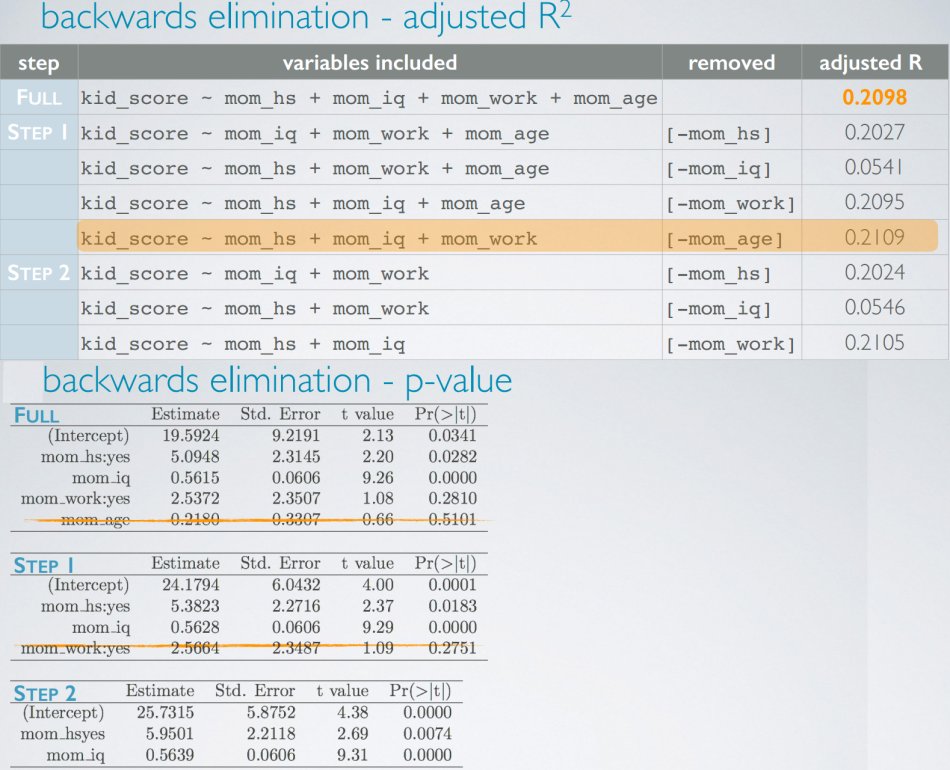
逐步模型选择
- 后向消除:从全模型(包含所有预测变量)开始,每次丢弃一个预测模型,直到获得精简模型
- 前向选择:从空模型开始,每次添加一个预测模型,直到获得精简模型
标准:
 调整变量的标准有两种:
调整变量的标准有两种:
- 使adjusted R square最大化;
- 使p-value最小化
如果存在反映同一个性质的一组分类变量,要么全部保留,要么全部去除,不可以保留不完整的一部分
诊断
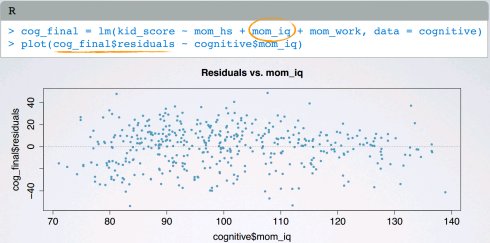
(1)(数字变量)x和y的线性关系
每个(数字)解释变量线性关联响应变量;
使用残差图检查残差是否随机分布0附近;不使用x和y的散点图,因为这样可以考虑模型内的其他变量,而不是仅仅x和y之间的二元变量关系。
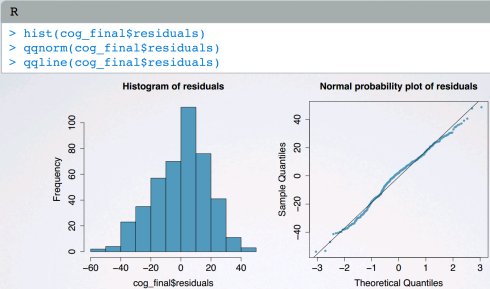
(2)近似均值为0的正态分布残差
某些残差为正,某些为负;在残差图中残差随机分布0附近;
使用直方图或正态概率图检查是否近似均值为0的正态分布残差
(3)残差的恒定可变性
残差应该对预测的响应变量的低值和高值有相等的可变性
使用residuals vs. predicted残差图检查:
residuals vs. predicted而不是residuals vs.x,允许一次考虑(带有所有解释变量的)整个模型;残差随机分布在0附件的常量带内;值得观察residuals vs.predicted的绝对值,轻松识别异常观察值。
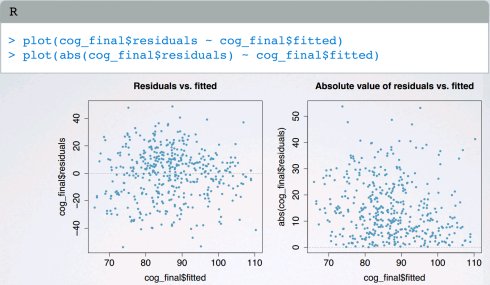
(4)独立的残差
独立残差->独立观察值
如果是可疑的时间序列结构,对比检查残差和数据采集顺序,否则,思考数据如何采样的。